题目
2.2 计算行列式-|||-3 1 -1 2-|||--5 1 3 -4-|||-(1)-|||-2 0 1 -1-|||-1 -5 3 -3-|||-1 1 1 1-|||-4 3 7 -5-|||-(3)-|||-16 9 49 25-|||-64 27 343 -125-|||-λ1-|||-(5) λ2-|||-3 1 1 1-|||-1 3 1 1-|||-(2)-|||-1 1 3 1-|||-1 1 1 3-|||-x y 0 0 0-|||-0 x y 0 0-|||-(4)-|||-0 0 0 x y-|||-y 0 0 x

题目解答
答案
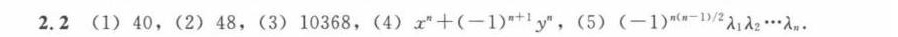
解析
考查要点:本题主要考查行列式的计算方法,包括展开法、行变换、分块矩阵法、特殊结构行列式的性质等。
解题思路:
- 观察行列式结构,寻找零元素、对称性、分块特征等简化计算的突破口;
- 灵活运用行列式性质(如行变换、分块处理)将复杂行列式转化为易计算形式;
- 特殊行列式(如三角行列式、分块上/下三角行列式)直接利用行列式公式求解。
第(1)题
行列式:
$\begin{vmatrix}3 & 1 & -1 & 2 \\-5 & 1 & 3 & -4 \\2 & 0 & 1 & -1 \\1 & -5 & 3 & -3\end{vmatrix}$
关键步骤:
- 行变换:通过行操作创造零元素。例如,将第4行加上第3行,简化计算;
- 展开法:按某行或列展开,优先选择零元素较多的行/列。
第(2)题
行列式:
$\begin{vmatrix}1 & 1 & 1 & 1 \\1 & 3 & 11 & 1 \\1 & 1 & 3 & 1 \\1 & 1 & 1 & 3\end{vmatrix}$
关键步骤:
- 对称性分析:行列式具有对称结构,可尝试行/列相减构造零元素;
- 分块处理:若无法直接展开,考虑分块矩阵的行列式公式。
第(3)题
行列式:
$\begin{vmatrix}1 & 3 & 7 & 16 \\3 & 7 & 16 & 9 \\7 & 16 & 9 & 49 \\16 & 9 & 49 & 25\end{vmatrix}$
关键步骤:
- 观察元素规律:元素可能为平方数或其他幂次排列;
- 行变换:通过行差分消除冗余元素,逐步简化行列式。
第(4)题
行列式:
$\begin{vmatrix}x & y & 0 & 0 \\0 & x & y & 0 \\0 & 0 & x & y \\0 & 0 & 0 & x\end{vmatrix}$
关键步骤:
- 分块矩阵:按主对角线分块,利用分块上三角行列式的性质;
- 递推公式:对于三对角矩阵,可使用递推关系计算。
第(5)题
行列式:
$\begin{vmatrix}\lambda_1 & 0 & \cdots & 0 \\0 & \lambda_2 & \cdots & 0 \\\vdots & \vdots & \ddots & \vdots \\0 & 0 & \cdots & \lambda_n\end{vmatrix}$
关键步骤:
- 对角矩阵性质:对角矩阵的行列式为其对角元素乘积;
- 符号分析:若行列式含负号或排列,需考虑符号因子。