题目
设随机变量 sim U(0,1), 当给定 X=x 时,随机变量Y的条件概率密-|||-度为 _(Y|x)(y|x)= { 0, .

题目解答
答案
解析
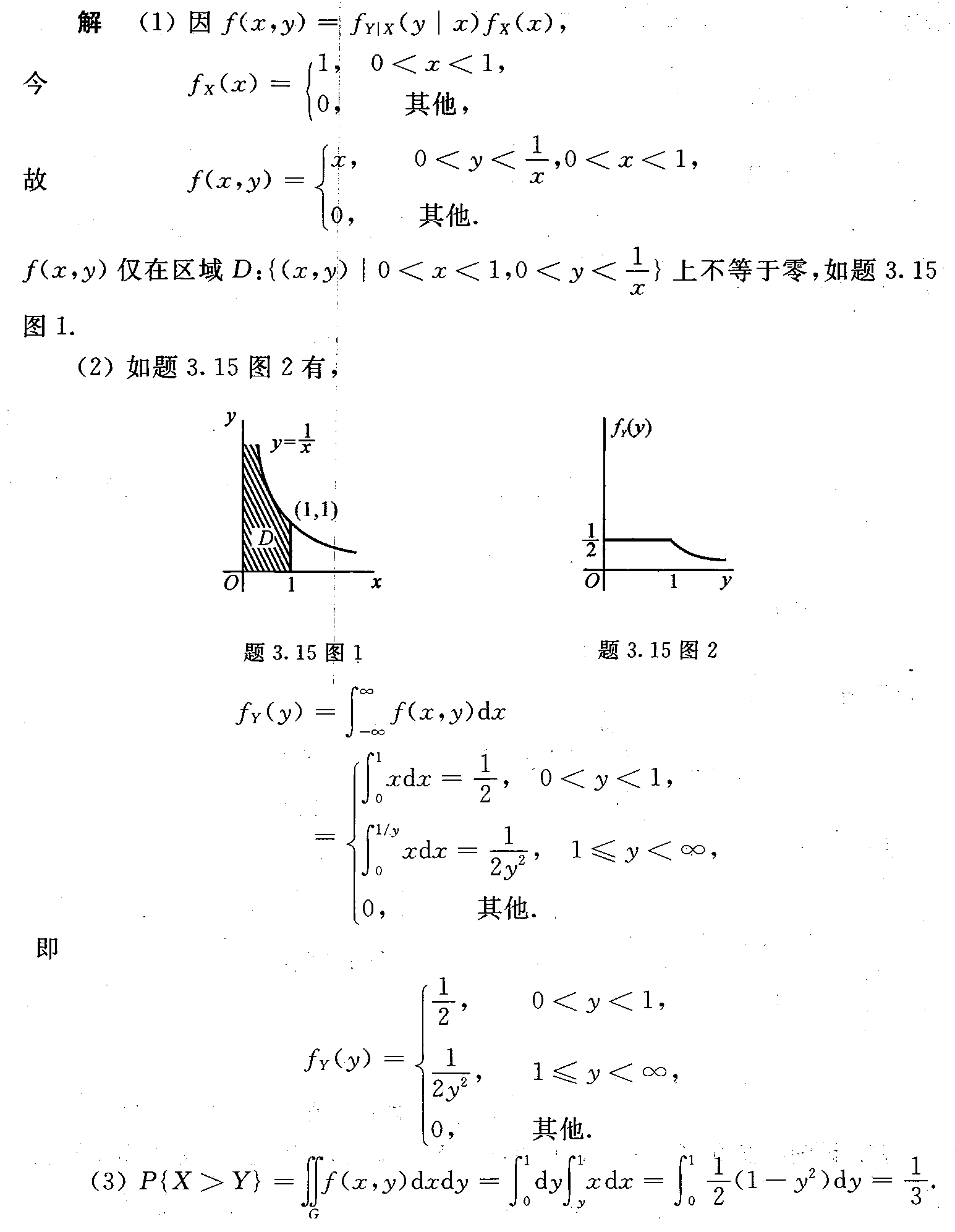
步骤 1:求联合概率密度f(x,y)
根据条件概率密度的定义,联合概率密度f(x,y)可以通过条件概率密度${f}_{Y|x}(y|x)$和边缘概率密度${f}_{X}(x)$的乘积得到。由于$X\sim U(0,1)$,所以${f}_{X}(x)=1$,$0$$f(x,y)={f}_{Y|x}(y|x)\cdot{f}_{X}(x)=x\cdot1=x$$
步骤 2:求边缘密度${f}_{Y}(y)$
边缘密度${f}_{Y}(y)$可以通过对联合概率密度f(x,y)在x的范围内积分得到。根据联合概率密度的定义,$0$${f}_{Y}(y)=\int_{0}^{1}f(x,y)dx=\int_{0}^{1}xdx$$
步骤 3:求$P\{X>Y\}$
$P\{X>Y\}$可以通过对联合概率密度f(x,y)在$X>Y$的区域上积分得到。根据联合概率密度的定义,$0Y\}$为:
$$P\{X>Y\}=\int_{0}^{1}\int_{0}^{x}f(x,y)dydx$$
根据条件概率密度的定义,联合概率密度f(x,y)可以通过条件概率密度${f}_{Y|x}(y|x)$和边缘概率密度${f}_{X}(x)$的乘积得到。由于$X\sim U(0,1)$,所以${f}_{X}(x)=1$,$0
步骤 2:求边缘密度${f}_{Y}(y)$
边缘密度${f}_{Y}(y)$可以通过对联合概率密度f(x,y)在x的范围内积分得到。根据联合概率密度的定义,$0
步骤 3:求$P\{X>Y\}$
$P\{X>Y\}$可以通过对联合概率密度f(x,y)在$X>Y$的区域上积分得到。根据联合概率密度的定义,$0
$$P\{X>Y\}=\int_{0}^{1}\int_{0}^{x}f(x,y)dydx$$