(1)若曲线 =(x)^2+ax+b 与 =x(y)^3-1 在点 (1,-1) 处相切,则常数a,b是-|||-() .-|||-A. =0, , b=-2 B. =1, , b=-3-|||-C. =-3, , b=1 D. a=-1 , b=-1
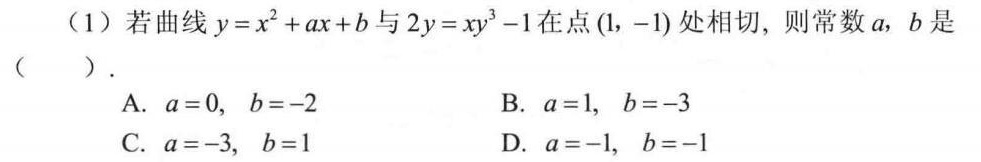
题目解答
答案
解析
考查要点:本题主要考查曲线在某点相切的条件,即两曲线在该点有相同的函数值和相同的导数。需要综合运用函数值代入和隐函数求导的方法。
解题思路:
- 验证点(1,-1)是否在两条曲线上,代入方程求解参数关系。
- 分别求两条曲线在该点的导数,令导数相等,建立方程。
- 联立方程求解参数a和b。
破题关键:
- 相切条件:函数值相等且导数相等。
- 隐函数求导:对第二条曲线使用隐函数求导法则,注意链式法则的应用。
验证点(1,-1)在两条曲线上
第一条曲线 $y = x^2 + ax + b$
代入点$(1, -1)$:
$-1 = 1^2 + a \cdot 1 + b \implies 1 + a + b = -1 \implies \boxed{a + b = -2} \quad \text{(方程1)}$
第二条曲线 $2y = xy^3 - 1$
代入点$(1, -1)$:
$2 \cdot (-1) = 1 \cdot (-1)^3 - 1 \implies -2 = -1 - 1 \implies \text{成立}$
求两条曲线在点(1,-1)处的导数
第一条曲线的导数
$y' = 2x + a \quad \xrightarrow{x=1} \quad y'(1) = 2 + a$
第二条曲线的导数(隐函数求导)
对 $2y = xy^3 - 1$ 两边求导:
$2 \frac{dy}{dx} = y^3 + 3xy^2 \frac{dy}{dx}$
整理得:
$\frac{dy}{dx} = \frac{y^3}{2 - 3xy^2}$
代入点$(1, -1)$:
$\frac{dy}{dx} = \frac{(-1)^3}{2 - 3 \cdot 1 \cdot (-1)^2} = \frac{-1}{2 - 3} = 1$
联立方程求解a和b
根据导数相等:
$2 + a = 1 \implies a = -1$
代入方程1:
$-1 + b = -2 \implies b = -1$