题目
3.2 计算积分 (int )_(c)dfrac (overline {z)}(|z|)dz 的值,其中C为(1) |z|=2 ;(2) |z|=4. .

题目解答
答案
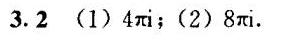
解析
考查要点:本题主要考查复变函数沿闭曲线的积分计算,涉及复数共轭、模长的参数化处理,以及利用参数方程法计算复积分。
解题核心思路:
- 参数化曲线:将圆周路径$|z|=r$表示为$z(t)=r e^{it}$,其中$t \in [0, 2\pi)$。
- 化简被积函数:利用共轭复数$\overline{z}=r e^{-it}$和模长$|z|=r$,将被积函数转化为关于$t$的表达式。
- 计算积分:通过参数替换,将复积分转化为关于$t$的实积分,最终得到结果。
破题关键点:
- 正确参数化:确保$z(t)$和$dz$的表达式正确。
- 化简技巧:利用指数形式简化共轭复数与模长的运算。
- 积分计算:注意积分区间和复数单位$i$的处理。
第(1)题:$|z|=2$
-
参数化曲线:
设$z(t)=2 e^{it}$,其中$t \in [0, 2\pi]$,则$dz = i \cdot 2 e^{it} dt$。 -
化简被积函数:
- $\overline{z} = 2 e^{-it}$,$|z|=2$,故$\dfrac{\overline{z}}{|z|} = \dfrac{2 e^{-it}}{2} = e^{-it}$。
- 被积函数变为$e^{-it} \cdot i \cdot 2 e^{it} = 2i$。
-
计算积分:
$\int_{C} \dfrac{\overline{z}}{|z|} dz = \int_{0}^{2\pi} 2i \, dt = 2i \cdot 2\pi = 4\pi i$
第(2)题:$|z|=4$
-
参数化曲线:
设$z(t)=4 e^{it}$,其中$t \in [0, 2\pi]$,则$dz = i \cdot 4 e^{it} dt$。 -
化简被积函数:
- $\overline{z} = 4 e^{-it}$,$|z|=4$,故$\dfrac{\overline{z}}{|z|} = \dfrac{4 e^{-it}}{4} = e^{-it}$。
- 被积函数变为$e^{-it} \cdot i \cdot 4 e^{it} = 4i$。
-
计算积分:
$\int_{C} \dfrac{\overline{z}}{|z|} dz = \int_{0}^{2\pi} 4i \, dt = 4i \cdot 2\pi = 8\pi i$