16.求极限 lim _(xarrow 0)dfrac (sqrt {1+xsin x)-sqrt (cos x)}({x)^2}
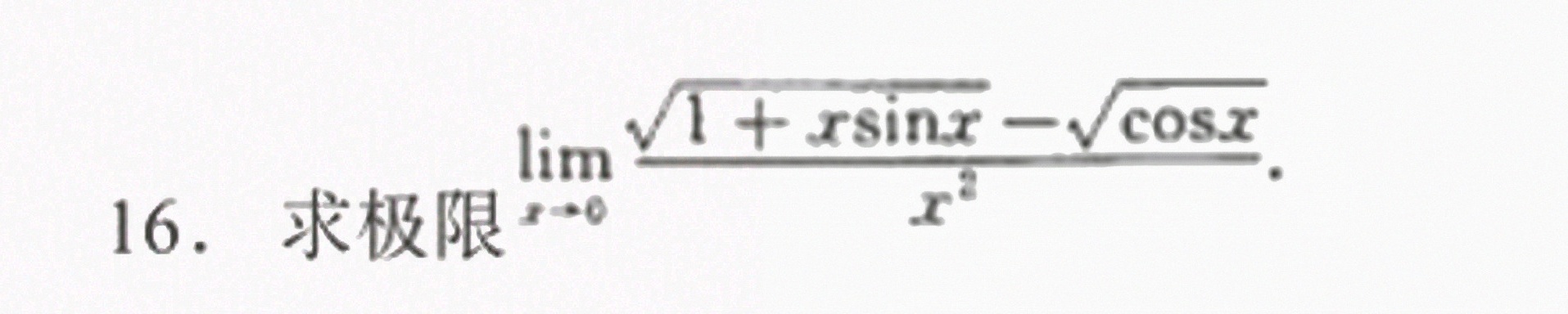
题目解答
答案
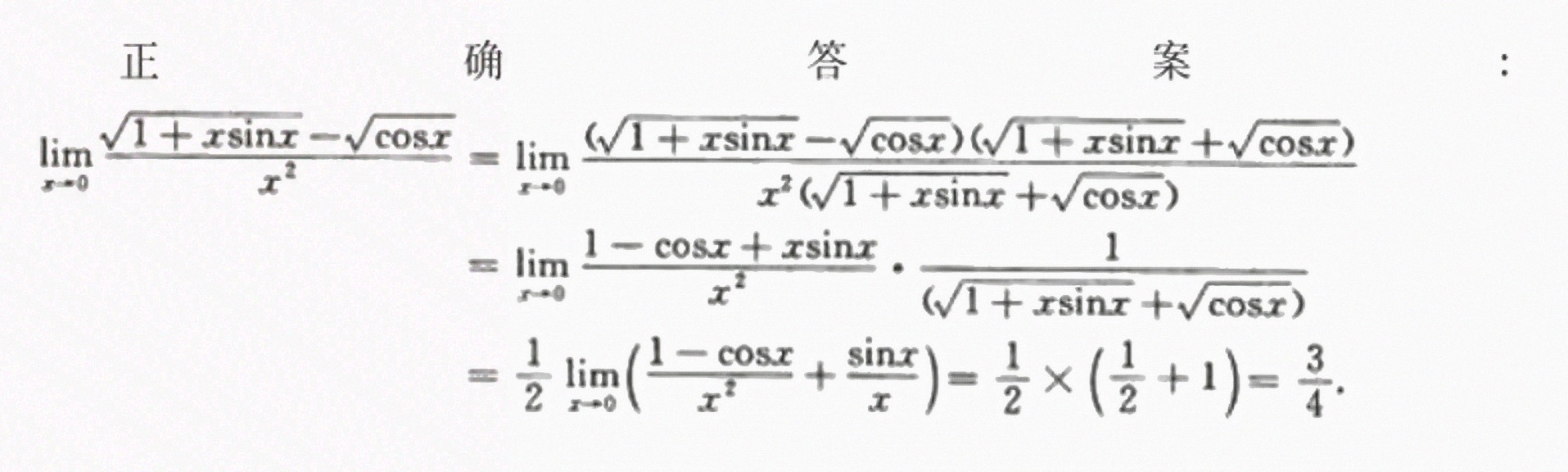
解析
考查要点:本题主要考查极限的计算方法,特别是处理根号相减的有理化技巧,以及利用常见极限公式进行化简的能力。
解题核心思路:
当分子为两个根号相减时,通常通过分子有理化消除根号,将原式转化为更易处理的形式。随后,结合常见极限公式(如$\lim_{x \to 0} \frac{1 - \cos x}{x^2} = \frac{1}{2}$和$\lim_{x \to 0} \frac{\sin x}{x} = 1$)进行分步计算。
破题关键点:
- 分子有理化:通过乘以共轭表达式,将分子转化为多项式形式。
- 拆分极限:将化简后的表达式拆分为两个部分,分别计算各自的极限值。
- 代入已知极限:利用基本极限公式简化计算过程。
步骤1:分子有理化
原式为:
$\lim _{x\rightarrow 0}\dfrac {\sqrt {1+x\sin x}-\sqrt {\cos x}}{{x}^{2}}$
将分子乘以共轭表达式$\sqrt{1+x\sin x} + \sqrt{\cos x}$,分母同步乘以相同表达式:
$\begin{aligned}\text{原式} &= \lim _{x\rightarrow 0} \dfrac{(\sqrt{1+x\sin x} - \sqrt{\cos x})(\sqrt{1+x\sin x} + \sqrt{\cos x})}{x^2 (\sqrt{1+x\sin x} + \sqrt{\cos x})} \\&= \lim _{x\rightarrow 0} \dfrac{(1 + x\sin x) - \cos x}{x^2 (\sqrt{1+x\sin x} + \sqrt{\cos x})}.\end{aligned}$
步骤2:化简分子
分子部分展开为:
$1 + x\sin x - \cos x = (1 - \cos x) + x\sin x.$
因此,原式变为:
$\lim _{x\rightarrow 0} \dfrac{1 - \cos x + x\sin x}{x^2 (\sqrt{1+x\sin x} + \sqrt{\cos x})}.$
步骤3:拆分极限
将表达式拆分为两部分:
$\lim _{x\rightarrow 0} \dfrac{1 - \cos x + x\sin x}{x^2} \cdot \dfrac{1}{\sqrt{1+x\sin x} + \sqrt{\cos x}}.$
分别计算两部分的极限:
- 第一部分:
$\lim _{x\rightarrow 0} \dfrac{1 - \cos x}{x^2} + \dfrac{x\sin x}{x^2} = \dfrac{1}{2} + 1 = \dfrac{3}{2}.$
(利用$\lim_{x \to 0} \frac{1 - \cos x}{x^2} = \frac{1}{2}$和$\lim_{x \to 0} \frac{\sin x}{x} = 1$) - 第二部分:
$\lim _{x\rightarrow 0} \dfrac{1}{\sqrt{1+x\sin x} + \sqrt{\cos x}} = \dfrac{1}{1 + 1} = \dfrac{1}{2}.$
步骤4:合并结果
两部分相乘得:
$\dfrac{3}{2} \cdot \dfrac{1}{2} = \dfrac{3}{4}.$