题目
(3) lim _(xarrow 0)dfrac (tan x-sin x)({sin )^3x}
题目解答
答案
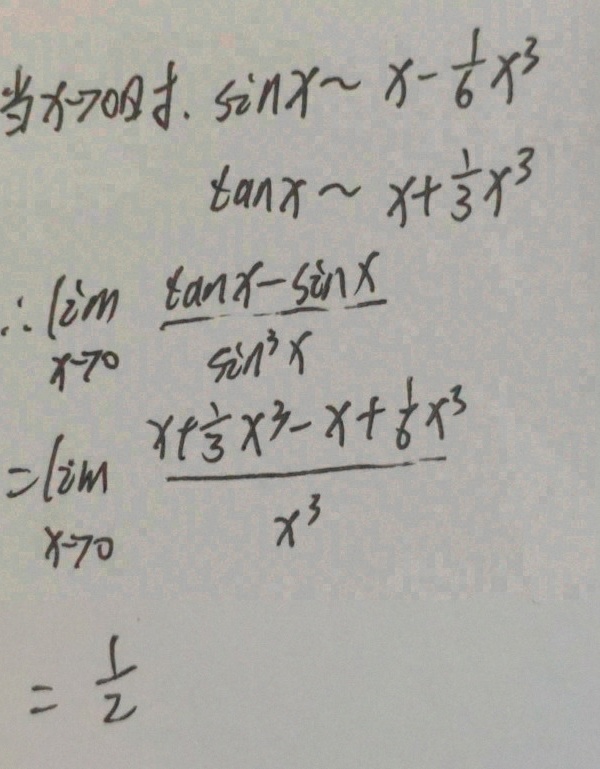
解析
考查要点:本题主要考查利用等价无穷小替换或泰勒展开求解极限的能力,重点在于对三角函数在$x \rightarrow 0$时的展开式的掌握。
解题核心思路:
当$x \rightarrow 0$时,$\sin x$和$\tan x$都可以展开为泰勒多项式。通过展开分子$\tan x - \sin x$和分母$\sin^3 x$,保留到$x^3$项,再进行约简即可求得极限。
破题关键点:
- 正确展开$\sin x$和$\tan x$的泰勒多项式到$x^3$项;
- 准确计算分子和分母的高阶小项,并化简;
- 约去相同阶数的无穷小量,得到最终结果。
步骤1:展开分子$\tan x - \sin x$
根据泰勒展开式:
- $\sin x = x - \dfrac{1}{6}x^3 + o(x^3)$
- $\tan x = x + \dfrac{1}{3}x^3 + o(x^3)$
因此:
$\begin{aligned}\tan x - \sin x &= \left( x + \dfrac{1}{3}x^3 \right) - \left( x - \dfrac{1}{6}x^3 \right) + o(x^3) \\&= \dfrac{1}{3}x^3 + \dfrac{1}{6}x^3 + o(x^3) \\&= \dfrac{1}{2}x^3 + o(x^3)\end{aligned}$
步骤2:展开分母$\sin^3 x$
利用$\sin x \sim x$(当$x \rightarrow 0$时),可得:
$\sin^3 x \sim x^3$
步骤3:计算极限
将分子和分母代入原式:
$\lim_{x \rightarrow 0} \dfrac{\tan x - \sin x}{\sin^3 x} = \lim_{x \rightarrow 0} \dfrac{\dfrac{1}{2}x^3 + o(x^3)}{x^3} = \dfrac{1}{2}$