4. 求由坐标平面及 x=2 =3, x+y+z=4 所-|||-围的角柱体的体积.
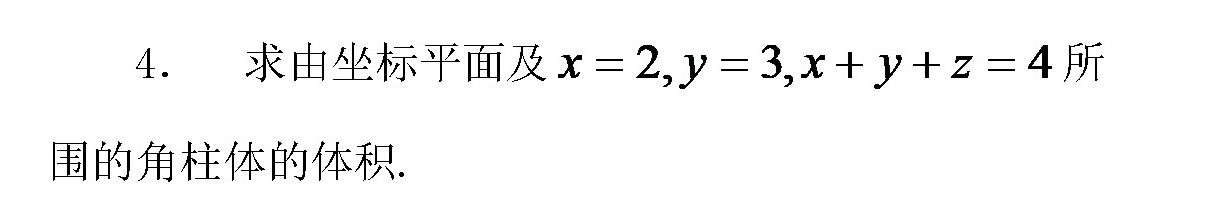
题目解答
答案
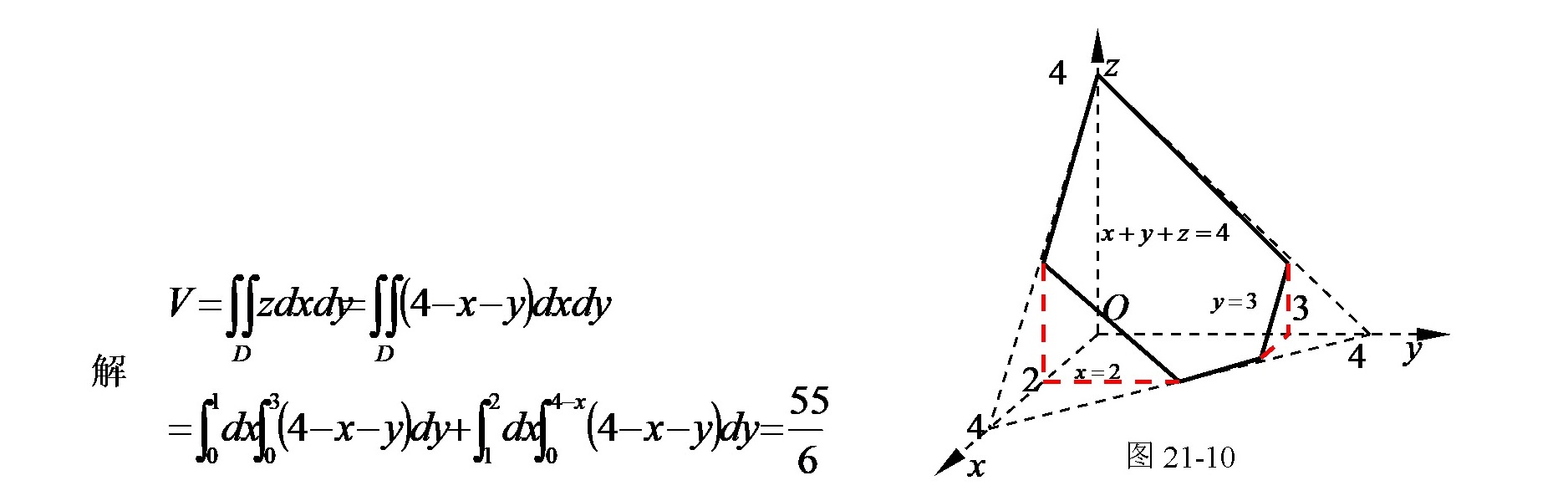
解析
本题考查利用二重积分求空间立体体积的知识,核心思路是通过确定积分区域,将体积转化为目标函数在该区域上的二重积分进行计算计算。
步骤1:确定积分区域D
所求立体由坐标平面($x=0,y=0,z=0$、$x=2$、$y=3$、$x+y+z=4$围成,是一个柱体。
- 投影区域D:在$xy$-平面上的投影,由$x=0,x=2,y=0,y=3$及$z=0$时$x+y\leq4$(因$z=4-x-y\geq0\Rightarrow y\leq4-x$)围成。
- 分两部分:
① $x\in[0,1]$时,$y\in[0,3]$($4-x\geq3$);
② $V=\iint_D(4-x-y)dxdy=\int_0^1dx\int_0^3(4-x-y)dy+\int_1^2dx\int_0^{4-x}(4-x-y)dy$。
- 分两部分:
步骤2:计算二重积分
第一部分($x\in[0,1]$)
$\int_0^1dx\int_0^3(4-x-y)dy=\int_0^1\left[(4-x)y-\frac{1}{2}y^2\right]_0^3dx=\int_0^1\left[3(4-x)-\frac{9}{2}\right]dx=\int_0^1\left(\frac{15}{2}-3x\right)dx=\left[\frac{15}{2}x-\frac{3}{2}{2}\right]_0^1=\frac{15}{2}-\frac{3}{2}=6$
**
$\int_1^2dx\int_0^{4-x}(4-x-y)dy=\int_1^2\left[(4-x)y-\frac{1}{2}y^2\right]_0^{4-x}dx=\int_1^2\left[\frac{1}{2}(4-x)^2\right]dx=\frac{1}{2}\int_1^2(4-x)^2dx$
令$t=4-x$,则$dt=-dx$,积分变为:
$\frac{1}{2}\int_3^2t^2dt=\frac{1}{2}\left[-\frac{1}{3}t^3\right]_3^2=\frac{1}{2}\left(-\frac{8}{3}+\frac{27}{3}\right)=\frac{19}{6}$
步骤3:总和得体积
$V=6+\frac{19}{6}=\frac{36}{6}{6}+\frac{19}{6}=\frac{55}{6}$