题目
抛物面=dfrac (1)(2)((x)^2+(y)^2) 被平面 =dfrac (1)(2)((x)^2+(y)^2)所截下有限部分的面积是=dfrac (1)(2)((x)^2+(y)^2)( A ) =dfrac (1)(2)((x)^2+(y)^2)( B ) =dfrac (1)(2)((x)^2+(y)^2)( C ) =dfrac (1)(2)((x)^2+(y)^2)( D ) =dfrac (1)(2)((x)^2+(y)^2)
抛物面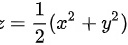
被平面 
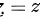所截下有限部分的面积是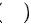
( A )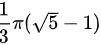 
( B )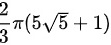 
( C )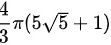 
( D )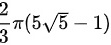 
题目解答
答案
答案：选D
依题意，设
抛物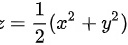面 被平面 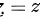所截下有限部分为
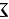，其在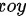
平面的投影为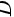
∴
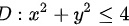
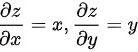
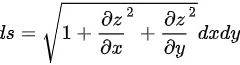
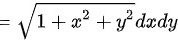
曲面的面积为：
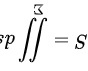
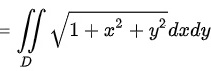
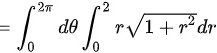
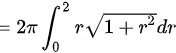
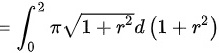
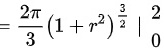
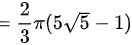
故，D选项正确，A、B、C错误
解析
步骤 1：确定曲面和投影区域
抛物面$z=\dfrac {1}{2}({x}^{2}+{y}^{2})$ 被平面 $z=4$ 所截下有限部分的投影区域为 $D:{x}^{2}+{y}^{2}\leqslant 4$，即半径为2的圆。
步骤 2：计算曲面的面积元素
曲面的面积元素为 ${s}_{s}=\sqrt {1+\dfrac {\partial {z}^{2}}{\partial x}+\dfrac {\partial {z}^{2}}{\partial y}}dxdy$，其中 $\dfrac {\partial z}{\partial x}=x$，$\dfrac {\partial z}{\partial y}=y$，因此 ${s}_{s}=\sqrt {1+{x}^{2}+{y}^{2}}dxdy$。
步骤 3：计算曲面的面积
曲面的面积为 $S=\iint \sqrt {1+{x}^{2}+{y}^{2}}dxdy$，在极坐标下，$x=r\cos \theta$，$y=r\sin \theta$，$dxdy=rdrd\theta$，因此 $S=2\pi \int _{0}^{2}r\sqrt {1+r^{2}}dr$。
步骤 4：计算积分
$S=2\pi \int _{0}^{2}r\sqrt {1+r^{2}}dr=2\pi \int _{0}^{2}\dfrac {1}{2}\sqrt {1+r^{2}}d(1+r^{2})=2\pi \dfrac {1}{3}(1+r^{2})^{\dfrac {3}{2}}|_{0}^{2}=\dfrac {2}{3}\pi (5\sqrt {5}-1)$。
抛物面$z=\dfrac {1}{2}({x}^{2}+{y}^{2})$ 被平面 $z=4$ 所截下有限部分的投影区域为 $D:{x}^{2}+{y}^{2}\leqslant 4$，即半径为2的圆。
步骤 2：计算曲面的面积元素
曲面的面积元素为 ${s}_{s}=\sqrt {1+\dfrac {\partial {z}^{2}}{\partial x}+\dfrac {\partial {z}^{2}}{\partial y}}dxdy$，其中 $\dfrac {\partial z}{\partial x}=x$，$\dfrac {\partial z}{\partial y}=y$，因此 ${s}_{s}=\sqrt {1+{x}^{2}+{y}^{2}}dxdy$。
步骤 3：计算曲面的面积
曲面的面积为 $S=\iint \sqrt {1+{x}^{2}+{y}^{2}}dxdy$，在极坐标下，$x=r\cos \theta$，$y=r\sin \theta$，$dxdy=rdrd\theta$，因此 $S=2\pi \int _{0}^{2}r\sqrt {1+r^{2}}dr$。
步骤 4：计算积分
$S=2\pi \int _{0}^{2}r\sqrt {1+r^{2}}dr=2\pi \int _{0}^{2}\dfrac {1}{2}\sqrt {1+r^{2}}d(1+r^{2})=2\pi \dfrac {1}{3}(1+r^{2})^{\dfrac {3}{2}}|_{0}^{2}=\dfrac {2}{3}\pi (5\sqrt {5}-1)$。