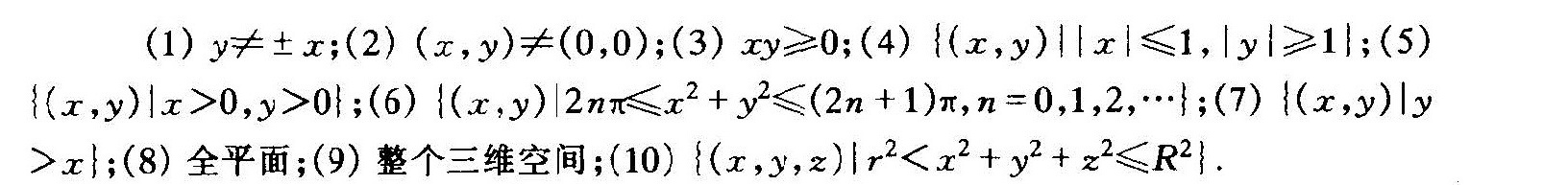题目
求下列各函数的定义域,画出定义域的图形,并说明这是何种点集:(1)f(x,y)=dfrac({x)^2+(y)^2}({x)^2-(y)^2}(2)f(x,y)=dfrac(1)(2{x)^2+3(y)^2}(3)f(x,y)=sqrt(xy)(4)f(x,y)=sqrt(1-(x)^2)+sqrt((y)^2-1)(5)f(x,y)=ln x+ln y(6)f(x,y)=sqrt(sin ((x)^2+{y)^2)}(7)f(x,y)=ln (y-x)(8)f(x,y)=(e)^-((x^2+{y)^2)}(9)f(x,y,z)=dfrac(z)({x)^2+(y)^2+1}(10)f(x,y,z)=sqrt((R)^2-{x)^2-(y)^2-(z)^2}+dfrac(1)(sqrt({x)^2+{y)^2+(z)^2-(r)^2}}(Rgt r)
求下列各函数的定义域,画出定义域的图形,并说明这是何种点集:
$\left(1\right)$$f\left(x,y\right)=\dfrac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$
$\left(2\right)$$f\left(x,y\right)=\dfrac{1}{2{x}^{2}+3{y}^{2}}$
$\left(3\right)$$f\left(x,y\right)=\sqrt{xy}$
$\left(4\right)$$f\left(x,y\right)=\sqrt{1-{x}^{2}}+\sqrt{{y}^{2}-1}$
$\left(5\right)$$f\left(x,y\right)=\ln x+\ln y$
$\left(6\right)$$f\left(x,y\right)=\sqrt{\sin \left({x}^{2}+{y}^{2}\right)}$
$\left(7\right)$$f\left(x,y\right)=\ln \left(y-x\right)$
$\left(8\right)$$f\left(x,y\right)={e}^{-\left({x}^{2}+{y}^{2}\right)}$
$\left(9\right)$$f\left(x,y,z\right)=\dfrac{z}{{x}^{2}+{y}^{2}+1}$
$\left(10\right)$$f\left(x,y,z\right)=\sqrt{{R}^{2}-{x}^{2}-{y}^{2}-{z}^{2}}+\dfrac{1}{\sqrt{{x}^{2}+{y}^{2}+{z}^{2}-{r}^{2}}}\left(R\gt r\right)$
题目解答
答案