题目
6.给出函数表1.13.作出差商表,作出三次Newton 插值多项式,并计算f(1.2)的近似值.-|||-表1.13-|||-x -1.00 2.00 3.00 4.00-|||-f(x) 3.00 5.00 7.00 5.00

题目解答
答案
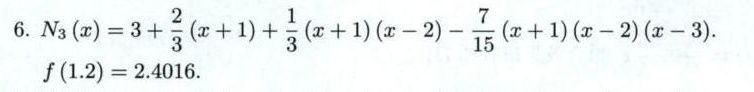
解析
考查要点:本题主要考查牛顿插值法的应用,包括差商表的构造和三次牛顿插值多项式的建立,以及利用多项式进行函数值近似计算的能力。
解题核心思路:
- 差商计算:通过递推方式计算各阶差商,构建差商表。
- 多项式构造:根据差商值,按照牛顿插值多项式的形式逐项累加。
- 代入求值:将目标点代入多项式,分步计算各阶项的值并求和。
破题关键点:
- 差商公式的正确应用,注意分母为节点间距。
- 多项式展开时的基函数形式,即$(x-x_0)(x-x_1)\cdots(x-x_{k-1})$。
- 计算精度控制,避免中间步骤的四舍五入误差累积。
差商表构造
| 节点 | $x_0=-1$ | $x_1=2$ | $x_2=3$ | $x_3=4$ |
|---|---|---|---|---|
| $f(x)$ | 3.00 | 5.00 | 7.00 | 5.00 |
| 一阶差商 | $\frac{2}{3}$ | $2$ | $-2$ | |
| 二阶差商 | $\frac{1}{3}$ | $-2$ | ||
| 三阶差商 | $-\frac{7}{15}$ |
三次牛顿插值多项式
形式为:
$y_3(x) = f[x_0] + f[x_0,x_1](x-x_0) + f[x_0,x_1,x_2](x-x_0)(x-x_1) + f[x_0,x_1,x_2,x_3](x-x_0)(x-x_1)(x-x_2)$
代入差商值:
$y_3(x) = 3 + \frac{2}{3}(x+1) + \frac{1}{3}(x+1)(x-2) - \frac{7}{15}(x+1)(x-2)(x-3)$
计算$f(1.2)$
将$x=1.2$代入多项式:
- 第一项:$3$
- 第二项:$\frac{2}{3}(1.2+1) = \frac{2}{3} \times 2.2 \approx 1.4667$
- 第三项:$\frac{1}{3}(2.2)(1.2-2) = \frac{1}{3} \times 2.2 \times (-0.8) \approx -0.5867$
- 第四项:$-\frac{7}{15}(2.2)(-0.8)(1.2-3) = -\frac{7}{15} \times 3.168 \approx -1.4784$
求和:
$3 + 1.4667 - 0.5867 - 1.4784 = 2.4016$