题目
一直线和直二面角的两个面所成的角分别是α,β,则α+β的范围是( )A.itB.itC.itD.it
一直线和直二面角的两个面所成的角分别是α,β,则α+β的范围是( )
- A.
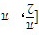
- B.
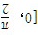
- C.
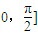
- D.
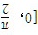
题目解答
答案
【答案】这题可以从直线与平面的位置出发,分三种情况讨论:
①如果它与两个平面都相交,那么它和两个平面的角,恰是直角三角形的两个锐角.通过比较三角函数值,可以得到:α+β<90°
②如果这直线与两个半平面都平行,那么它与两个面的角都是0°,故α+β=0°.
③如果它只与一个面垂直,那么它与一个面的角是90°,而与另一个面的角是0°,故α+β=90°.
①如果它与两个平面都相交,那么它和两个平面的角,恰是直角三角形的两个锐角.通过比较三角函数值,可以得到:α+β<90°
②如果这直线与两个半平面都平行,那么它与两个面的角都是0°,故α+β=0°.
③如果它只与一个面垂直,那么它与一个面的角是90°,而与另一个面的角是0°,故α+β=90°.
解析
考查要点:本题主要考查直线与直二面角两个面所成角的关系,需要结合空间几何中直线与平面夹角的定义及直二面角的性质进行分析。
解题核心思路:
- 明确直二面角的定义:由两个互相垂直的平面组成的二面角。
- 理解直线与平面夹角的定义:直线与平面中垂直于该直线在平面上的投影线所形成的锐角。
- 分类讨论:根据直线与两个平面的位置关系(相交、平行、垂直等),分析α和β的可能取值,进而确定α+β的范围。
破题关键点:
- 极端情况分析:当直线与两个平面平行时,α+β=0°;当直线与其中一个平面垂直时,α+β=90°。
- 一般情况分析:当直线与两个平面均相交时,α和β的和不超过90°,可通过几何模型或向量方法验证。
情况分析
1. 直线与两个平面均相交
设直二面角的两个平面为α₁和α₂,直线L与α₁、α₂分别成角α和β。
- 几何模型:直线L在两个平面内的投影形成直角三角形,α和β为该三角形的两个锐角。
- 结论:α + β ≤ 90°(当直线沿两平面交线的对角线方向时,α + β = 90°)。
2. 直线与两个平面均平行
- 几何模型:直线L与两个平面均无交点,平行于两平面。
- 结论:α = 0°,β = 0°,故α + β = 0°。
3. 直线与其中一个平面垂直
- 几何模型:直线L垂直于平面α₁,则α = 90°,且L在平面α₂内的投影与α₂平行,故β = 0°。
- 结论:α + β = 90°。
综合范围
通过上述三种情况可知,α + β的最小值为0°,最大值为90°,因此范围为 [0, π/2]。