题目
求平行于向量overrightarrow (a)=(6,7,-6)单位向量_______
求平行于向量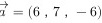 单位向量_______
单位向量_______
题目解答
答案
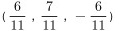 或
或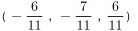
解析
考查要点:本题主要考查单位向量的求解方法以及向量平行的条件。
解题思路:
- 单位向量的定义是方向与原向量相同或相反,且模长为1的向量。
- 平行向量的条件是方向相同或相反,因此单位向量可以是原向量的正方向或负方向。
- 关键步骤:先计算原向量的模长,再用原向量的每个分量除以模长,最后考虑正负两种情况。
步骤1:计算向量$\overrightarrow{a}$的模长
向量$\overrightarrow{a} = (6, 7, -6)$的模长公式为:
$\|\overrightarrow{a}\| = \sqrt{6^2 + 7^2 + (-6)^2} = \sqrt{36 + 49 + 36} = \sqrt{121} = 11$
步骤2:求单位向量
单位向量的公式为$\frac{\overrightarrow{a}}{\|\overrightarrow{a}\|}$,因此:
$\text{单位向量} = \left( \frac{6}{11}, \frac{7}{11}, \frac{-6}{11} \right)$
步骤3:考虑平行方向
平行向量包括方向相同和相反两种情况,因此单位向量还可以是上述结果的相反数:
$\text{单位向量} = \left( -\frac{6}{11}, -\frac{7}{11}, \frac{6}{11} \right)$