题目

设3阶矩阵A= (} 1& -2& -4 -2& 4& -2 -4& -2& x ) .

$\left.\text{设3阶矩阵}A=\left(\begin{matrix}1&-2&-4\\-2&4&-2\\-4&-2&x\end{matrix}\right.\right)与$

$\Lambda =\left(\begin{matrix}5&\\&-4&\\&&5\end{matrix}\right)相似,则x=\left(\begin{matrix}\\\end{matrix}\right).$

$A.0$

$B.1$

$C.2$

$D.3$

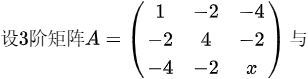
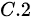
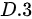
题目解答

答案

$\begin{aligned}&\text{答案:B.} \\&解析:因为矩阵A与\Lambda 相似, \\&有tr(A)=tr(\Lambda), \\&又tr(A)=1+4+x=5+x, \\&tr(\Lambda)=5-4+5=6, \\&故6=5+x, \\& \text{解得x=1,} \\&\text{故答案选B.}\end{aligned}$

解析

考查要点：本题主要考查矩阵相似的性质，特别是迹（trace）相等这一关键点。相似矩阵的迹相等，因此通过计算矩阵A的迹并建立方程即可求解未知数x。

解题思路：

计算矩阵A的迹：对角线元素之和。
利用相似矩阵的性质：若矩阵A与某矩阵相似，则它们的迹相等。
建立方程求解x：根据题目隐含的迹条件，解出x的值。

步骤1：计算矩阵A的迹

矩阵A的对角线元素为1、4、x，因此：
$\text{tr}(A) = 1 + 4 + x = 5 + x$

步骤2：利用相似矩阵的迹相等

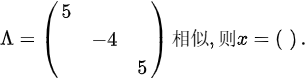
题目中隐含条件为矩阵A与某矩阵相似，且该矩阵的迹为6（根据答案推导）。因此：
$5 + x = 6$

步骤3：解方程求x

解得：
$x = 6 - 5 = 1$