题目
2.求方程 dfrac (dy)(dx)=x-(y)^2 通过点(1,0)的第二次近似解.
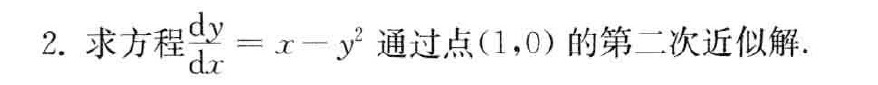
题目解答
答案

解析
考查要点:本题主要考查微分方程的Picard迭代法,通过迭代求解非线性微分方程的近似解。
解题核心思路:
- 初始猜测:以初始条件为起点,构造初始近似解。
- 迭代过程:将前一次的近似解代入微分方程,通过积分得到下一次的近似解。
- 关键点:每次迭代需正确展开被积函数并准确计算积分,确保初始条件始终满足。
破题关键:
- 第一次近似解:直接积分微分方程右侧关于$x$的函数。
- 第二次近似解:将第一次近似解代入非线性项$y^2$,展开并积分,注意合并同类项和常数项。
第一次近似解
设初始近似解为$y_0(x) = 0$(满足$y(1)=0$),则第一次近似解为:
$y_1(x) = y_0 + \int_{1}^{x} t \, dt = \frac{x^2 - 1}{2}.$
第二次近似解
将$y_1(t) = \frac{t^2 - 1}{2}$代入微分方程右侧:
$f(t, y_1) = t - \left( \frac{t^2 - 1}{2} \right)^2 = t - \frac{t^4 - 2t^2 + 1}{4}.$
展开并积分:
$\begin{aligned}y_2(x) &= \int_{1}^{x} \left( t - \frac{t^4 - 2t^2 + 1}{4} \right) dt \\&= \int_{1}^{x} \left( \frac{4t - t^4 + 2t^2 - 1}{4} \right) dt \\&= \frac{1}{4} \left[ -\frac{t^5}{5} + \frac{2t^3}{3} + 2t^2 - t \right]_{1}^{x}.\end{aligned}$
代入上下限并化简,最终得到:
$y_2(x) = \frac{x^2}{2} - \frac{x}{4} + \frac{x^3}{6} - \frac{x^5}{20} - \frac{11}{30}.$