题目
4.设曲线积分 (int )_(L)[ (e)^x+f(x)] ydx+f(x)dy 与路径无关,其中f (x)是连续可微函数且满足 f(0)=1 ,-|||-求f(x).

题目解答
答案
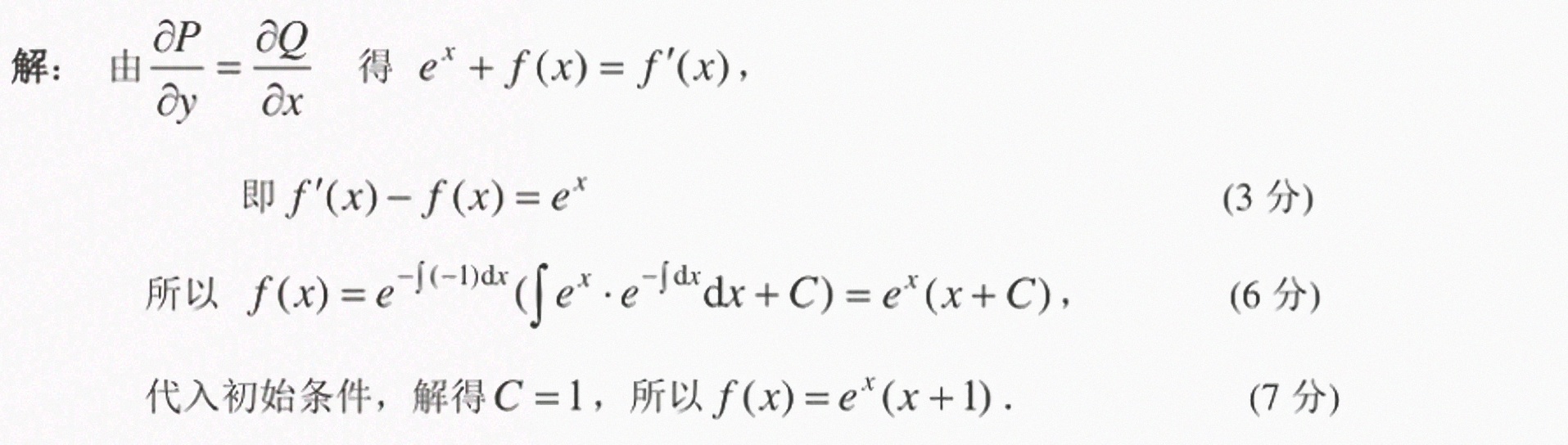
解析
步骤 1:确定积分与路径无关的条件
曲线积分 ${\int }_{L}[ {e}^{x}+f(x)] ydx+f(x)dy$ 与路径无关,意味着积分的值只依赖于起点和终点,而与路径无关。根据格林定理,这等价于积分的被积函数满足 $\dfrac {\partial P}{\partial y}=\dfrac {\partial Q}{\partial x}$,其中 $P=[ {e}^{x}+f(x)] y$,$Q=f(x)$。
步骤 2:计算偏导数并建立方程
计算 $\dfrac {\partial P}{\partial y}=\dfrac {\partial }{\partial y}([ {e}^{x}+f(x)] y)=[ {e}^{x}+f(x)]$,以及 $\dfrac {\partial Q}{\partial x}=\dfrac {\partial }{\partial x}f(x)=f'(x)$。根据步骤1中的条件,我们有 $[ {e}^{x}+f(x)]=f'(x)$,即 $f'(x)-f(x)={e}^{x}$。
步骤 3:求解微分方程
这是一个一阶线性微分方程,可以使用积分因子法求解。积分因子为 ${e}^{-x}$,乘以方程两边得到 ${e}^{-x}f'(x)-{e}^{-x}f(x)={e}^{-x}{e}^{x}=1$。左边是 ${e}^{-x}f(x)$ 的导数,因此 $\dfrac {d}{dx}({e}^{-x}f(x))=1$。积分得到 ${e}^{-x}f(x)=x+C$,其中 C 是积分常数。因此,$f(x)={e}^{x}(x+C)$。
步骤 4:确定常数 C
根据题目条件 $f(0)=1$,代入 $f(x)={e}^{x}(x+C)$ 得到 $1={e}^{0}(0+C)=C$。因此,$C=1$。
曲线积分 ${\int }_{L}[ {e}^{x}+f(x)] ydx+f(x)dy$ 与路径无关,意味着积分的值只依赖于起点和终点,而与路径无关。根据格林定理,这等价于积分的被积函数满足 $\dfrac {\partial P}{\partial y}=\dfrac {\partial Q}{\partial x}$,其中 $P=[ {e}^{x}+f(x)] y$,$Q=f(x)$。
步骤 2:计算偏导数并建立方程
计算 $\dfrac {\partial P}{\partial y}=\dfrac {\partial }{\partial y}([ {e}^{x}+f(x)] y)=[ {e}^{x}+f(x)]$,以及 $\dfrac {\partial Q}{\partial x}=\dfrac {\partial }{\partial x}f(x)=f'(x)$。根据步骤1中的条件,我们有 $[ {e}^{x}+f(x)]=f'(x)$,即 $f'(x)-f(x)={e}^{x}$。
步骤 3:求解微分方程
这是一个一阶线性微分方程,可以使用积分因子法求解。积分因子为 ${e}^{-x}$,乘以方程两边得到 ${e}^{-x}f'(x)-{e}^{-x}f(x)={e}^{-x}{e}^{x}=1$。左边是 ${e}^{-x}f(x)$ 的导数,因此 $\dfrac {d}{dx}({e}^{-x}f(x))=1$。积分得到 ${e}^{-x}f(x)=x+C$,其中 C 是积分常数。因此,$f(x)={e}^{x}(x+C)$。
步骤 4:确定常数 C
根据题目条件 $f(0)=1$,代入 $f(x)={e}^{x}(x+C)$ 得到 $1={e}^{0}(0+C)=C$。因此,$C=1$。