题目
[题目]函数 (x)=dfrac (sqrt {{x)^2-9}}(x-3)+ln (1+x) 的定义域是
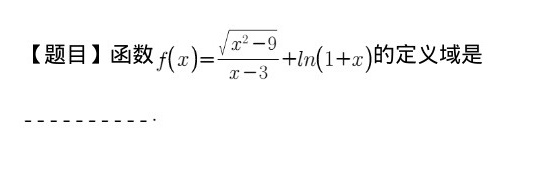
题目解答
答案

解析
步骤 1:确定根号内表达式的非负性
${x}^{2}-9\geqslant 0$,解得 $x\leqslant -3$ 或 $x\geqslant 3$。
步骤 2:确定分母不为零
$x-3\neq 0$,解得 $x\neq 3$。
步骤 3:确定对数函数的定义域
$1+x\gt 0$,解得 $x\gt -1$。
步骤 4:综合以上条件,确定函数的定义域
结合以上三个条件,解得 $x\gt 3$。
${x}^{2}-9\geqslant 0$,解得 $x\leqslant -3$ 或 $x\geqslant 3$。
步骤 2:确定分母不为零
$x-3\neq 0$,解得 $x\neq 3$。
步骤 3:确定对数函数的定义域
$1+x\gt 0$,解得 $x\gt -1$。
步骤 4:综合以上条件,确定函数的定义域
结合以上三个条件,解得 $x\gt 3$。