题目
6.3人独立地去破译一份密码,已知各人能译出的概率分别为 https:/img.zuoyebang.cc/zyb_45dc0d89990e93bcf633c09040976484.jpg/5, 1/3 ,1/4. 问3人中至少有一人能-|||-将此密码译出的概率是多少?

题目解答
答案
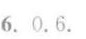
解析
考查要点:本题主要考查独立事件的概率计算,特别是利用逆事件概率简化问题的思路。
解题核心思路:
题目要求“至少有一人成功”的概率,直接计算需要考虑多种情况(恰好1人成功、恰好2人成功、3人均成功),较为复杂。因此,转化为计算“所有人都失败”的概率,再用1减去该概率,更为简便。
破题关键点:
- 确定各人失败的概率:成功概率分别为$\frac{1}{5}$、$\frac{1}{3}$、$\frac{1}{4}$,则失败概率分别为$\frac{4}{5}$、$\frac{2}{3}$、$\frac{3}{4}$。
- 独立事件的乘积:三人均失败的概率为各人失败概率的乘积。
- 逆事件转换:用1减去均失败的概率,即得至少一人成功的概率。
步骤1:计算各人失败的概率
- 第一人失败的概率:$1 - \frac{1}{5} = \frac{4}{5}$
- 第二人失败的概率:$1 - \frac{1}{3} = \frac{2}{3}$
- 第三人失败的概率:$1 - \frac{1}{4} = \frac{3}{4}$
步骤2:计算三人均失败的概率
由于三人独立工作,均失败的概率为:
$\frac{4}{5} \times \frac{2}{3} \times \frac{3}{4} = \frac{4 \times 2 \times 3}{5 \times 3 \times 4} = \frac{24}{60} = \frac{2}{5}$
步骤3:计算至少一人成功的概率
用1减去均失败的概率:
$1 - \frac{2}{5} = \frac{3}{5} = 0.6$