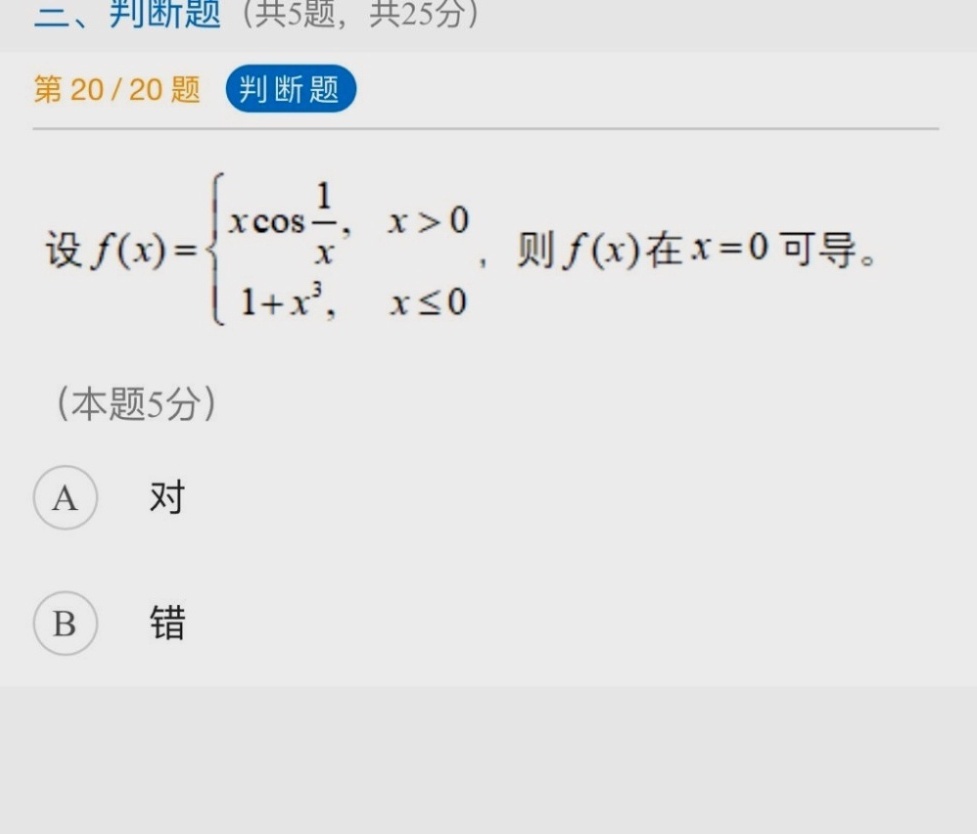
二、判断题(共5题,共25分)-|||-第 20/20 题 判断题-|||-设 f(x)= , xgt 0 1+{x)^3, xleqslant 0 . ,则f(x)在 x=0 可导。-|||-(本题5分)-|||-A 对-|||-B 错

考查要点：本题主要考查分段函数在分段点处的可导性判断，需要综合运用函数连续性和导数定义的知识。

解题核心思路：

1. 判断函数在$x=0$处是否连续：若不连续，则直接不可导；
2. 若连续，则计算左右导数，验证是否相等。

破题关键点：

• 连续性是可导的前提，若函数在$x=0$处不连续，可直接判定不可导；
• 右极限$\lim_{x \to 0^+} f(x)$的计算需注意$x \cos \frac{1}{x}$的极限性质。

步骤1：判断连续性

• 当$x \to 0^-$时：$f(x) = 1 + x^3$，极限为$\lim_{x \to 0^-} (1 + x^3) = 1$；
• 当$x \to 0^+$时：$f(x) = x \cos \frac{1}{x}$，由于$|\cos \frac{1}{x}| \leq 1$，故$|x \cos \frac{1}{x}| \leq |x|$，当$x \to 0^+$时，极限为$0$；
• 函数值$f(0)$：由定义$f(0) = 1 + 0^3 = 1$。

结论：左极限为$1$，右极限为$0$，且$f(0) = 1$，因此函数在$x=0$处不连续。

步骤2：可导性判断

由于函数在$x=0$处不连续，根据可导必连续的性质，$f(x)$在$x=0$处不可导。