填空⑴ 在顺序表[1]中,等概率情况下,插入和删除一个元素平均需移动( )个元素,具体移动元素的个数与( )和( )有关。[解答]表长的一半,表长,该元素在表中的位置⑵ 顺序表中第一个元素的存储地址是100,每个元素的长度为2,则第5个元素的存储地址是( )。[解答]108[分析]第5个元素的存储地址=第1个元素的存储地址+(5-1)×2=108⑶ 设单链表[2]中指针p 指向结点[3]A,若要删除A的后继结点(假设A存在后继结点),则需修改指针的操作为( )。[解答]p->next=(p->next)->next⑷ 单链表中设置头结点的作用是( )。[解答]为了运算方便[分析]例如在插入和删除操作时不必对表头的情况进行特殊处理。⑸ 非空的单循环链表[4]由头指针head指示,则其尾结点(由指针p所指)满足( )。[解答]p->next=head[分析]如图2-8所示。a1 a2 an p-|||-ead-|||-图 2-8 尾结点p与头指针head的关系示意图⑹ 在由尾指针rear指示的单循环链表中,在表尾插入一个结点s的操作序列是( );删除开始结点的操作序列为( )。[解答]s->next =rear->next; rear->next =s; rear =s;(将S的指针域先弄成表尾指针域,而表尾指针域是代表下个结点的地址信息,所以要将指针域要用S替代,最后把表尾给S)q=rear->next->next; rear->next->next=q->next; delete q;[分析]操作示意图如图2-9所示:a1 a2 an p-|||-ead-|||-图 2-8 尾结点p与头指针head的关系示意图⑺ 一个具有n个结点的单链表,在指针p所指结点后插入一个新结点的时间复杂度为( );在给定值为x的结点后插入一个新结点的时间复杂度为( )。[解答]Ο(1),Ο(n)[分析]在p所指结点后插入一个新结点只需修改指针,所以时间复杂度为Ο(1)(是表示常数计算时间);而在给定值为x的结点后插入一个新结点需要先查找值为x的结点,所以时间复杂度为Ο(n)。⑻ 设数组S[n]作为两个栈S1和S2的存储空间,对任何一个栈只有当S[n]全满时才不能进行进栈操作。为这两个栈分配空间的最佳方案是( )。A. S1的栈底位置为0,S2的栈底位置为n-1 B. S1的栈底位置为0,S2的栈底位置为n/2 C. S1的栈底位置为0,S2的栈底位置为n D. S1的栈底位置为0,S2的栈底位置为1 E. [解答]A F. [分析]两栈共享空间首先两个栈是相向增长的,栈底应该分别指向两个栈中的第一个元素的位置,并注意C++中的数组下标是从0开始的。 G. ⑼ 设有两个串p和q,求q在p中首次出现的位置的运算称作( )。 连接 模式匹配 求子串 求串长 [解答]B
填空
⑴ 在顺序表[1]中,等概率情况下,插入和删除一个元素平均需移动( )个元素,具体移动元素的个数与( )和( )有关。
[解答]表长的一半,表长,该元素在表中的位置
⑵ 顺序表中第一个元素的存储地址是100,每个元素的长度为2,则第5个元素的存储地址是( )。
[解答]108
[分析]第5个元素的存储地址=第1个元素的存储地址+(5-1)×2=108
⑶ 设单链表[2]中指针p 指向结点[3]A,若要删除A的后继结点(假设A存在后继结点),则需修改指针的操作为( )。
[解答]p->next=(p->next)->next
⑷ 单链表中设置头结点的作用是( )。
[解答]为了运算方便
[分析]例如在插入和删除操作时不必对表头的情况进行特殊处理。
⑸ 非空的单循环链表[4]由头指针head指示,则其尾结点(由指针p所指)满足( )。
[解答]p->next=head
[分析]如图2-8所示。

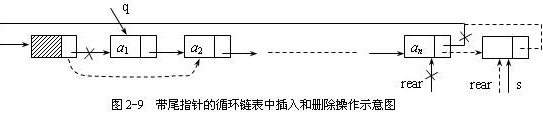
⑹ 在由尾指针rear指示的单循环链表中,在表尾插入一个结点s的操作序列是( );删除开始结点的操作序列为( )。
[解答]s->next =rear->next; rear->next =s; rear =s;(将S的指针域先弄成表尾指针域,而表尾指针域是代表下个结点的地址信息,所以要将指针域要用S替代,最后把表尾给S)
q=rear->next->next; rear->next->next=q->next; delete q;
[分析]操作示意图如图2-9所示:
⑺ 一个具有n个结点的单链表,在指针p所指结点后插入一个新结点的时间复杂度为( );在给定值为x的结点后插入一个新结点的时间复杂度为( )。
[解答]Ο(1),Ο(n)
[分析]在p所指结点后插入一个新结点只需修改指针,所以时间复杂度为Ο(1)(是表示常数计算时间);而在给定值为x的结点后插入一个新结点需要先查找值为x的结点,所以时间复杂度为Ο(n)。
⑻ 设数组S[n]作为两个栈S1和S2的存储空间,对任何一个栈只有当S[n]全满时才不能进行进栈操作。为这两个栈分配空间的最佳方案是( )。
A. S1的栈底位置为0,S2的栈底位置为n-1B. S1的栈底位置为0,S2的栈底位置为n/2
C. S1的栈底位置为0,S2的栈底位置为n
D. S1的栈底位置为0,S2的栈底位置为1
E. [解答]A
F. [分析]两栈共享空间首先两个栈是相向增长的,栈底应该分别指向两个栈中的第一个元素的位置,并注意C++中的数组下标是从0开始的。
G. ⑼ 设有两个串p和q,求q在p中首次出现的位置的运算称作( )。
连接
模式匹配
求子串
求串长
[解答]B
题目解答
答案
A S1的栈底[5]位置为0,S2的栈底位置为n-1 B S1的栈底位置为0,S2的栈底位置为n/ 2 C S1的栈底位置为0,S2的栈底位置为n D S1的栈底位置为0,S2的栈底位置为1 【解答】A 【分析】两栈共享空间首先两个栈是相向增长的,栈底应该分别指向两个栈中的第一个元素的位置,并注意C++中的数组下标是从0开始的。 ⑼ 设有两个串p和q,求q在p中首次出现的位置的运算称作( )。 A 连接 B 模式匹配[6] C 求子串[7] D 求串长[8] 【解答】B
解析
本题主要考查了数据结构中顺序表、单链表、栈和串的相关知识,下面对每道题进行详细分析:
- 顺序表插入和删除元素的平均移动元素个数:
- 本题考查顺序表插入和删除操作的特性。解题思路是分别考虑在顺序表不同位置插入和删除元素时移动元素的个数,然后根据等概率情况计算平均值。
- 解析:在长度为 $n$ 的顺序表中,插入一个元素时,若插入到第 $i$ 个位置($1\leq i\leq n + 1$),需要移动 $n - i + 1$ 个元素;删除一个元素时,若删除第 $i$ 个位置($1\leq i\leq n$)的元素,需要移动 $n - i$ 个元素。等概率情况下,插入操作的平均移动元素个数为 $\frac{1}{n + 1}\sum_{i = 1}^{n + 1}(n - i + 1)=\frac{n}{2}$;删除操作的平均移动元素个数为 $\frac{1}{n}\sum_{i = 1}^{n}(n - i)=\frac{n - 1}{2}$。综合来看,平均需移动表长的一半个元素,具体移动元素的个数与表长和该元素在表中的位置有关。
- 顺序表中元素存储地址的计算:
- 本题考查顺序表存储地址的计算方法。解题思路是根据顺序表中元素存储地址的计算公式进行计算。
- 解析:顺序表中第 $i$ 个元素的存储地址计算公式为 $LOC(i)=LOC(1)+(i - 1)\times L$,其中 $LOC(1)$ 是第一个元素的存储地址,$L$ 是每个元素的长度。已知 $LOC(1)=100$,$L = 2$,$i = 5$,则 $LOC(5)=100+(5 - 1)\times2=108$。
- 单链表中删除指定结点的后继结点:
- 本题考查单链表的删除操作。解题思路是明确要删除的结点是指针 $p$ 所指结点的后继结点,通过修改指针来实现删除操作。
- 解析:要删除指针 $p$ 所指结点 $A$ 的后继结点,只需将 $p$ 的指针域指向其后继结点的后继结点,即 $p->next=(p->next)->next$。
- 单链表中设置头结点的作用:
- 本题考查单链表头结点的作用。解题思路是考虑单链表在进行插入和删除操作时,头结点对简化操作的影响。
- 解析:在单链表中设置头结点后,无论是在表头、表中还是表尾进行插入和删除操作,都可以统一处理,不必对表头的情况进行特殊判断,从而使运算更加方便。
- 非空单循环链表尾结点的特征:
- 本题考查单循环链表的结构特点。解题思路是根据单循环链表的定义,尾结点的指针域指向头指针。
- 解析:在非空的单循环链表中,尾结点的指针域指向头指针,即 $p->next = head$。
- 带尾指针的单循环链表的插入和删除操作:
- 本题考查带尾指针的单循环链表的插入和删除操作。解题思路是分别分析在表尾插入结点和删除开始结点时指针的修改情况。
- 解析:
- 在表尾插入一个结点 $s$ 时,首先将 $s$ 的指针域指向头结点(即 $rear->next$),然后将尾结点的指针域指向 $s$,最后更新尾指针为 $s$,操作序列为 $s->next = rear->next$;$rear->next = s$;$rear = s$。
- 删除开始结点时,先找到开始结点的后继结点 $q$(即 $q = rear->next->next$),然后将尾结点的指针域指向 $q$ 的后继结点,最后删除 $q$,操作序列为 $q = rear->next->next$;$rear->next->next = q->next$;$delete q$。
- 单链表插入操作的时间复杂度:
- 本题考查单链表插入操作的时间复杂度。解题思路是根据插入操作的具体过程,分析不同情况下的时间复杂度。
- 解析:
- 在指针 $p$ 所指结点后插入一个新结点,只需修改指针,不需要遍历链表,所以时间复杂度为 $O(1)$。
- 在给定值为 $x$ 的结点后插入一个新结点,需要先遍历链表查找值为 $x$ 的结点,平均需要遍历 $n/2$ 个结点,所以时间复杂度为 $O(n)$。
- 两栈共享存储空间的最佳方案:
- 本题考查两栈共享存储空间的分配策略。解题思路是考虑两栈相向增长的特点,选择合适的栈底位置。
- 解析:两栈共享空间时,两个栈是相向增长的,栈底应该分别指向两个栈中的第一个元素的位置。为了使空间利用率最高,S1 的栈底位置为 0,S2 的栈底位置为 $n - 1$,这样两个栈可以充分利用数组空间,直到数组全满才不能进行进栈操作。
- 串的模式匹配运算:
- 本题考查串的基本运算。解题思路是理解每个串运算的定义,根据题目描述判断对应的运算。
- 解析:求 $q$ 在 $p$ 中首次出现的位置的运算称作模式匹配,所以答案选 B。