(4) lim _(xarrow 0)((1+3{tan )^2x)}^(cot ^2x);
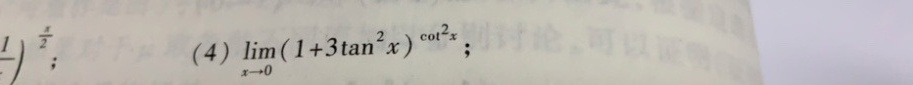
题目解答
答案
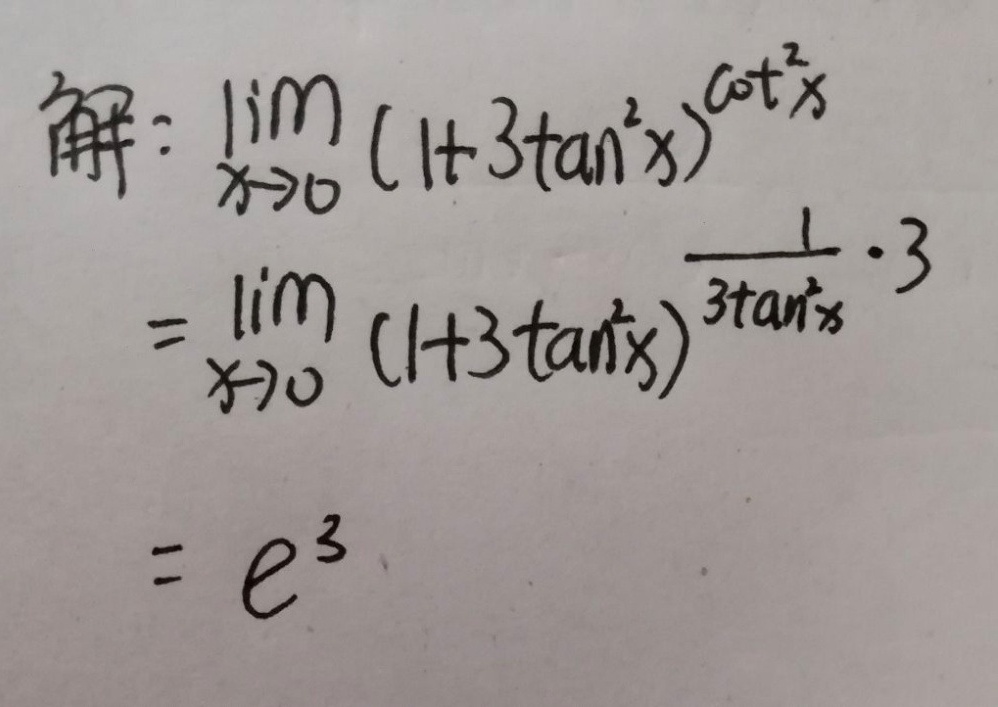
解析
题目1:${(-1)}^{\frac{3}{2}}$
该表达式涉及负数的分数指数幂,需先明确分数指数幂的定义:$a^{\frac{m}{n}}=\sqrt[n]{a^mm}$($n$为偶数时,$a$非负才有意义)。对于$(-1)^{\frac{3}{2}}$,等价于$\sqrt{(-1)^3}=\sqrt{-1}$,在实数范围内无意义(或视为复数$i$,但通常中学阶段默认实数域),题目可能重点在题目2。
题目2:$\lim _{x\rightarrow 0}{(1+3{\tan^{2}x)}^{cos^{2}x}$
本题考察重要极限:$\lim_{u \to 0}(1+u)^{\frac{1}{u}}=e$的推广应用,步骤如下:
-
凑重要极限形式:
令$t=3\tan^2x$,当$x \to 0$时,$\tan x \to 0$,故$t \to 0$。
原式$=(1+t)^{\cos^2x}$,需将指数转化为$\$\$\frac{1}{t}:
$\cos^2x=\frac{1}{\sec^2x}=\frac{1}{1+\tan^2x}=\frac{1}{1+\frac{t}{3}}$(因$t=3\tan^2x\Rightarrow\tan^2x=\frac{t}{3}$)。 -
指数变形:
$\cos^2x=\frac{3}{3+t}$,故原式$=(1+t)^{\frac{3}{3+t}}=\left[(1+t)^{\frac{1}{t}}\right]^{\frac{t\cdot\frac{3}{3+t}}\}}$。 -
取极限:
$\lim_{x \to 0}(1+t)^{\frac{1}{t}}=e$,$\lim_{x \to 0}\left(t\cdot\frac{3}{3+t}\right)}$=$\lim_{t \to 0}\frac{3t}{3+t}=0$,
由极限运算法则:原式$=e^3$。