题目
[题目]解不等式: ^2-5x+6lt 0.
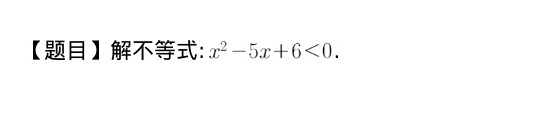
题目解答
答案
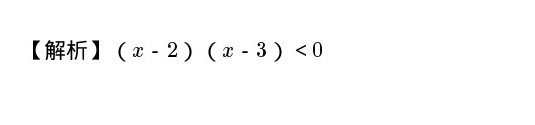
解析
考查要点:本题主要考查二次不等式的解法,涉及因式分解、二次函数图像性质的应用。
解题核心思路:
- 因式分解将二次不等式转化为两个一次因式的乘积形式;
- 根据二次函数的开口方向和根的位置,确定不等式成立的区间。
破题关键点:
- 正确分解因式:找到二次项系数为1时的两个数,使其积为常数项,和为一次项系数。
- 开口方向判断:二次项系数为正时,抛物线开口向上,此时不等式成立的区间位于两根之间。
步骤1:因式分解
将不等式 $x^2 -5x +6 < 0$ 分解为:
$(x-2)(x-3) < 0$
关键点:分解正确性验证:$(x-2)(x-3) = x^2 -5x +6$,与原式一致。
步骤2:确定根的位置
方程 $(x-2)(x-3) = 0$ 的根为 $x=2$ 和 $x=3$,将数轴分为三个区间:
- $x < 2$
- $2 < x < 3$
- $x > 3$
步骤3:分析开口方向
二次项系数为1(正数),抛物线开口向上,因此函数在两根之间取负值。
步骤4:确定解集
根据开口方向和根的位置,不等式 $(x-2)(x-3) < 0$ 的解集为:
$2 < x < 3$