题目
对应于实矩阵的相异特征值的实特征向量必是正交的。A.正确B.错误
对应于实矩阵的相异特征值的实特征向量必是正交的。
A.正确
B.错误
题目解答
答案
解:题干中说对应于实矩阵的相异特征值的实特征向量必是正交的。
而根据定理:实对称矩阵的不同特征值的特征向量是正交的。
我们可进行证明:
设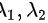 是
是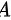 的两个不同的特征值,
的两个不同的特征值,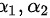 分别是其对应的特征向量
分别是其对应的特征向量
即有: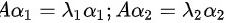
再两边取转置: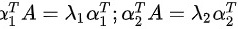
两边分别右乘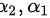 ,则有:
,则有:
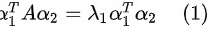
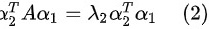
再对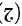 式两端取转置有:
式两端取转置有:
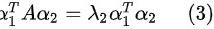
再由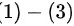 式得:
式得:
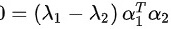
∵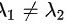 ∴
∴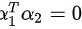
即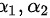 正交得证。
正交得证。
综上所述,此题表述错误,应选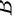 。
。
解析
考查要点:本题主要考查学生对矩阵特征向量正交性条件的理解,特别是对实矩阵与实对称矩阵性质的区分。
解题核心思路:
- 明确定理适用范围:实对称矩阵的不同特征值对应的特征向量正交,但这一性质仅适用于实对称矩阵,而非所有实矩阵。
- 反例验证:通过构造非对称实矩阵的实例,说明相异特征值的特征向量可能不正交。
破题关键点:
- 区分“实矩阵”与“实对称矩阵”的概念差异。
- 理解特征向量正交性的前提是矩阵满足特定条件(如对称性)。
错误原因分析:
题目中将“实对称矩阵”的性质错误推广到所有实矩阵。具体来说:
- 定理限定条件:只有实对称矩阵(或其他正规矩阵)的不同特征值对应的特征向量才正交。
- 一般实矩阵的性质:若矩阵不对称,则相异特征值的特征向量可能不正交。例如,取非对称实矩阵:
$A = \begin{bmatrix} 1 & 1 \\ 0 & 2 \end{bmatrix}$
其特征值为 $1$ 和 $2$,对应的特征向量分别为 $\begin{bmatrix}1 \\ 0\end{bmatrix}$ 和 $\begin{bmatrix}1 \\ 1\end{bmatrix}$,它们的点积为 $1 \cdot 1 + 0 \cdot 1 = 1 \neq 0$,说明不正交。
原证明的漏洞:
题目提供的证明过程隐含假设矩阵对称(如通过转置操作推导正交性),但未明确说明这一前提,导致结论错误。