14.设随机变量X的密度函数为-|||-.p(x)= , 0,|x|gt dfrac {pi )(2). .-|||-试求:-|||-(1)系数A;-|||-(2)X落在区间 (0,pi /4) 内的概率.

题目解答
答案
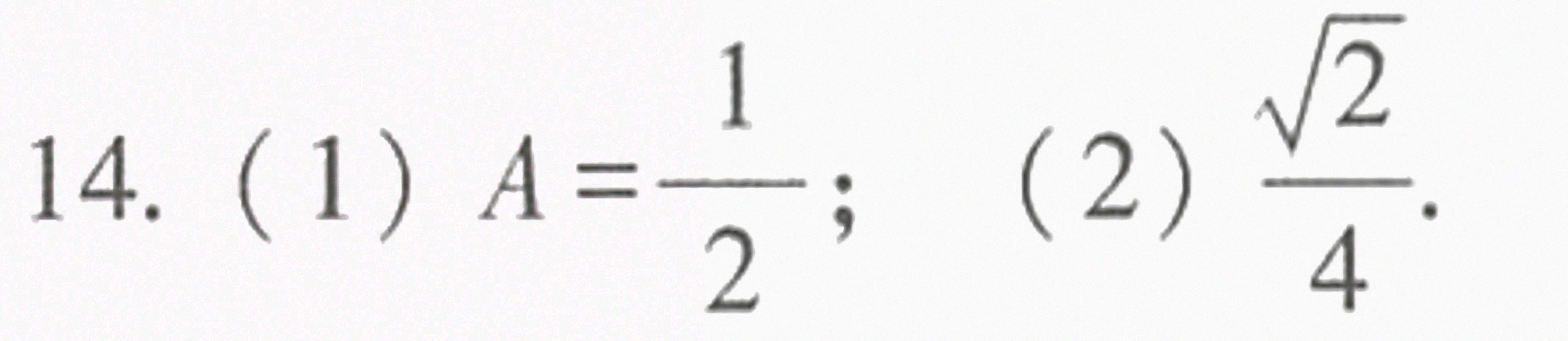
解析
考查要点:本题主要考查概率密度函数的性质及概率计算。
解题思路:
- 确定系数A:利用概率密度函数在整个定义域上的积分等于1的性质,建立方程求解。
- 计算概率:在已知密度函数的情况下,对指定区间积分即可得到概率。
关键点:
- 积分对称性:利用偶函数性质简化积分计算。
- 概率范围:概率结果必须满足$0 \leq P \leq 1$,若结果超出此范围需检查计算。
第(1)题:求系数A
根据概率密度函数的性质
概率密度函数$p(x)$在定义域上的积分等于1:
$\int_{-\infty}^{+\infty} p(x) \, dx = 1$
代入密度函数表达式
当$|x| \leq \frac{\pi}{2}$时,$p(x) = A \cos x$;否则$p(x) = 0$。因此积分区间为$[-\frac{\pi}{2}, \frac{\pi}{2}]$:
$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} A \cos x \, dx = 1$
利用偶函数性质简化积分
$\cos x$是偶函数,积分区间对称,可简化为:
$2A \int_{0}^{\frac{\pi}{2}} \cos x \, dx = 1$
计算积分
$2A \left[ \sin x \right]_0^{\frac{\pi}{2}} = 2A (\sin \frac{\pi}{2} - \sin 0) = 2A (1 - 0) = 2A$
解方程求A
$2A = 1 \implies A = \frac{1}{2}$
第(2)题:求$X$落在$(0, \frac{\pi}{4})$内的概率
概率计算公式
概率为密度函数在区间$(0, \frac{\pi}{4})$上的积分:
$P(0 < X < \frac{\pi}{4}) = \int_{0}^{\frac{\pi}{4}} p(x) \, dx$
代入已知密度函数
由第(1)题已求得$A = \frac{1}{2}$,因此:
$\int_{0}^{\frac{\pi}{4}} \frac{1}{2} \cos x \, dx$
计算积分
$\frac{1}{2} \left[ \sin x \right]_0^{\frac{\pi}{4}} = \frac{1}{2} \left( \sin \frac{\pi}{4} - \sin 0 \right) = \frac{1}{2} \left( \frac{\sqrt{2}}{2} - 0 \right) = \frac{\sqrt{2}}{4}$
结果验证
$\frac{\sqrt{2}}{4} \approx 0.3535$,符合概率范围$0 \leq P \leq 1$。