题目
下列方程是齐次微分方程的是（）A.'=2xyB. '=2xyC. '=2xyD. '=2xy
下列方程是齐次微分方程的是（）
A.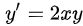
B.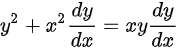 
C.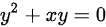 
D.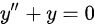 
题目解答
答案
∵本题要找的是齐次微分方程
∴分析选项A：A选项与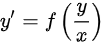
或者
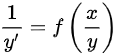形式不一样，故A错误。
分析选项B:等式两边同时除以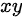
并移项得到
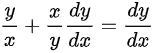
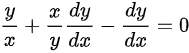
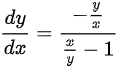与一般形式不符合，故选项B错误。
分析选项C：该方程是二元二次方程，不是微分方程，故选项C错误。
分析选项D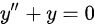：与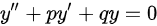
形式一致，故选项D正确。
故本题正确答案为D。
解析
步骤 1：分析选项A
A选项的方程为$y'=2xy$，这与齐次微分方程的一般形式$y'=f(\dfrac{y}{x})$或$\dfrac{1}{y'}=f(\dfrac{x}{y})$不一致，因此A选项不是齐次微分方程。
步骤 2：分析选项B
B选项的方程为${y}^{2}+{x}^{2}\dfrac{dy}{dx}=xy\dfrac{dy}{dx}$，等式两边同时除以$x^2$并移项得到$\dfrac{y}{x}+\dfrac{x}{y}\dfrac{dy}{dx}=\dfrac{dy}{dx}$，进一步整理得到$\dfrac{dy}{dx}=\dfrac{-\dfrac{y}{x}}{\dfrac{x}{y}-1}$，这与齐次微分方程的一般形式不一致，因此B选项不是齐次微分方程。
步骤 3：分析选项C
C选项的方程为${y}^{2}+xy=0$，这是一个二元二次方程，不是微分方程，因此C选项不是齐次微分方程。
步骤 4：分析选项D
D选项的方程为${y}^{11}+y=0$，这与二阶齐次线性微分方程的一般形式$y''+py'+qy=0$形式一致，因此D选项是齐次微分方程。
A选项的方程为$y'=2xy$，这与齐次微分方程的一般形式$y'=f(\dfrac{y}{x})$或$\dfrac{1}{y'}=f(\dfrac{x}{y})$不一致，因此A选项不是齐次微分方程。
步骤 2：分析选项B
B选项的方程为${y}^{2}+{x}^{2}\dfrac{dy}{dx}=xy\dfrac{dy}{dx}$，等式两边同时除以$x^2$并移项得到$\dfrac{y}{x}+\dfrac{x}{y}\dfrac{dy}{dx}=\dfrac{dy}{dx}$，进一步整理得到$\dfrac{dy}{dx}=\dfrac{-\dfrac{y}{x}}{\dfrac{x}{y}-1}$，这与齐次微分方程的一般形式不一致，因此B选项不是齐次微分方程。
步骤 3：分析选项C
C选项的方程为${y}^{2}+xy=0$，这是一个二元二次方程，不是微分方程，因此C选项不是齐次微分方程。
步骤 4：分析选项D
D选项的方程为${y}^{11}+y=0$，这与二阶齐次线性微分方程的一般形式$y''+py'+qy=0$形式一致，因此D选项是齐次微分方程。