题目
3.设(An)是一列集合,作 _(1)=(A)_(1), _(n)=(A)_(n)|(sum _(i=1)^n(A)_(i)) ,n=2, 3,..,证明(Bn)是一列互不相交的集合,-|||-而且 _(i=1)(A)_(i)=U(B)_(i) =1, 2,···
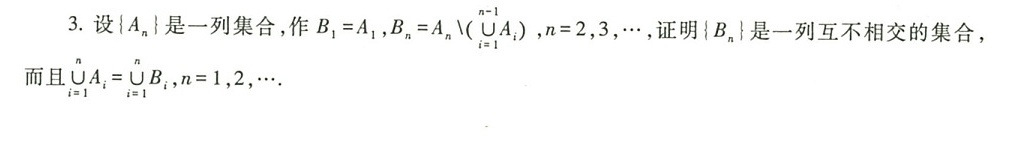
题目解答
答案

解析
本题主要考察集合的基本运算(并集集、差集)以及集合列的的性质,核心是证明构造的集合列$\{B_n\}$互不相交且与$\bigcup_{i=1}^{\inftyinfty}A_i$相等。
步骤1:证明$\{B_n\}$互不相交
任取$j < n$,需证$B_j \cap B_n = \ \emptyset$。
- 由定义:$B_j \subseteq A_j$,$B_n = A_n \setminus \bigcup_{i=1}^{n-1}A_i$(注意:题目中$U_{i-1}C_{i}A_{i}$应为$\bigcup_{i=1}^{n-1}A_i$的笔误,否则无法理解),故$B_n \subseteq A_n$且$B_n$与$\bigcup_{i=1}^{n-1}A_i$无交集。
- 因$j < n$,则$A_j \subseteq \bigcup_{i=1}^{n-1}A_i$,故$B_j \subseteq A_j \subseteq \bigcup_{i=1}^{n-1}A_i$,从而$B_j \cap B_n \subseteq (\bigcup_{i=1}^{n-1}A_i) \cap (A_n \setminus \bigcup_{i=1}^{n-1}A_i) = \emptyset$。
- 对任意$j \neq n$,同理可不妨设$j < n$,同理可证$B_n \cap B_j = \emptyset$,故$\{B_n$两两不交。
步骤2:证明$\bigcup_{i=1}^{\infty}A_i = \bigcup_{n=1}^{\infty}B_n$
(1)$\bigcup_{n=1}^{\infty}B_n \subseteq \bigcup_{i=1}^{\infty}A_i$
由定义$B_n \subseteq A_n$对所有$n$成立,故$\bigcup_{n=1}^{\infty}B_n \subseteq \bigcup_{n=1}^{\infty}A_n步骤(2)\(\bigcup_{i=1}^{\infty}A_i \subseteq \bigcup_{n=1}^{\infty}B_n$**
任取$x \in \bigcup_{i=1}^{\infty}A_i$,则存在最小自然数$k$使$x \in A_k$(最小性保证$x \notin \bigcup_{i=1}^{k-1}A_i$)。
由$B_k = A_k \setminus \bigcup_{i=1}^{k-1}A_i$,得$x \in B_k$,故$x \in \bigcup_{n=1}^{\infty}B_n$。
结论
$\{B_n\}$互不相交,且$\bigcup_{i=1}^{\infty}A_i = \bigcup_{n=1}^{\infty}B_n$。