题目
9、 int dfrac (1)(({x)^2+1)(x)^2}dx= __ 。
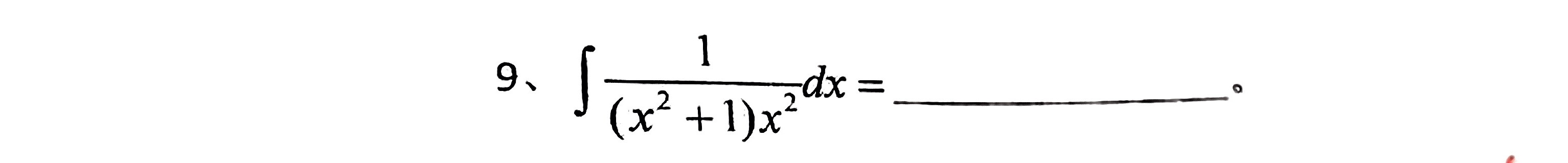
题目解答
答案
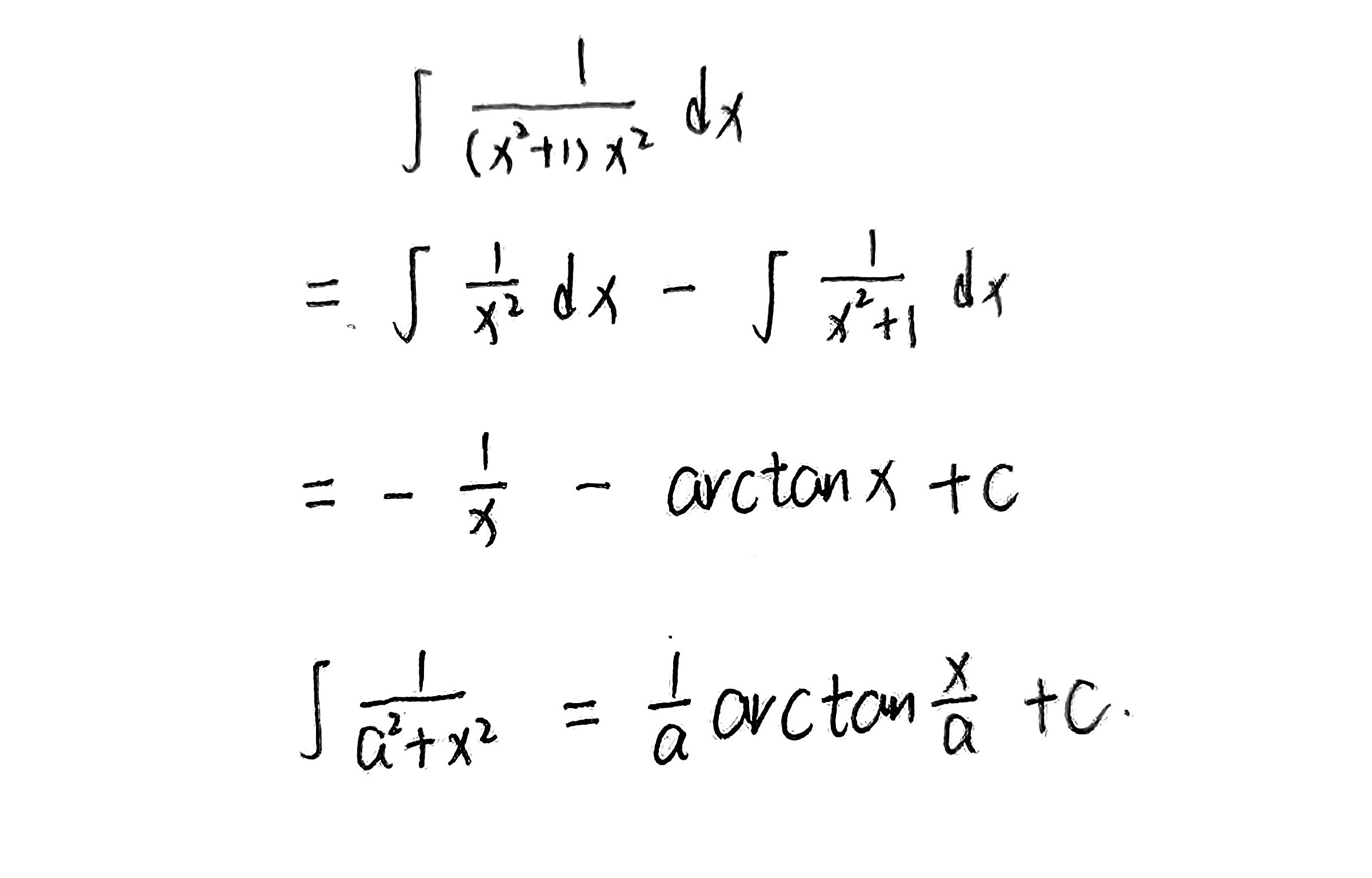
解析
步骤 1:分解被积函数
将被积函数 $\dfrac {1}{({x}^{2}+1){x}^{2}}$ 分解为两个部分,以便于积分。注意到 $\dfrac {1}{({x}^{2}+1){x}^{2}}$ 可以写成 $\dfrac {1}{{x}^{2}}-\dfrac {1}{{x}^{2}+1}$ 的形式。
步骤 2:积分
对分解后的函数进行积分。$\int \dfrac {1}{{x}^{2}}dx$ 的积分结果是 $-\dfrac {1}{x}+C_1$,而 $\int \dfrac {1}{{x}^{2}+1}dx$ 的积分结果是 $\arctan(x)+C_2$。
步骤 3:合并结果
将两个积分的结果合并,得到最终的积分结果。
将被积函数 $\dfrac {1}{({x}^{2}+1){x}^{2}}$ 分解为两个部分,以便于积分。注意到 $\dfrac {1}{({x}^{2}+1){x}^{2}}$ 可以写成 $\dfrac {1}{{x}^{2}}-\dfrac {1}{{x}^{2}+1}$ 的形式。
步骤 2:积分
对分解后的函数进行积分。$\int \dfrac {1}{{x}^{2}}dx$ 的积分结果是 $-\dfrac {1}{x}+C_1$,而 $\int \dfrac {1}{{x}^{2}+1}dx$ 的积分结果是 $\arctan(x)+C_2$。
步骤 3:合并结果
将两个积分的结果合并,得到最终的积分结果。