题目
4.已知曲线 y=f(x) 在点(0,0)处的切线过点(1,2),则-|||-lim _(xarrow 0)([ cos x+{int )_(0)^xf(t)dt] }^dfrac (1{{x)^2}}= __
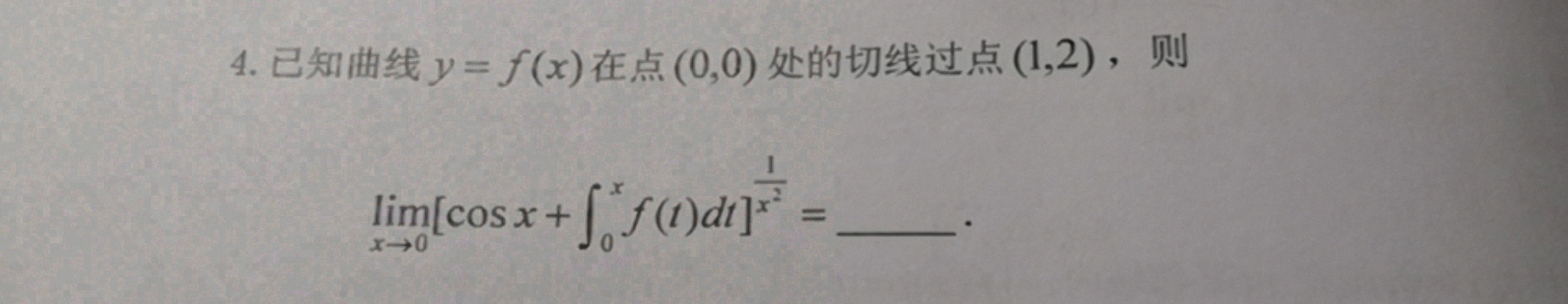
题目解答
答案

解析
步骤 1:确定切线方程
曲线 y=f(x) 在点 (0,0) 处的切线过点 (1,2),因此切线方程为 y=2x。由此可知 f(0)=0,f'(0)=2。
步骤 2:计算极限
考虑极限 $\lim _{x\rightarrow 0}{[ \cos x+{\int }_{0}^{x}f(t)dt] }^{\dfrac {1}{{x}^{2}}}$,首先计算 $\cos x+{\int }_{0}^{x}f(t)dt$ 在 x 趋近于 0 时的极限。
由于 $\lim _{x\rightarrow 0}\cos x=1$,且 $\lim _{x\rightarrow 0}{\int }_{0}^{x}f(t)dt=0$,因此 $\lim _{x\rightarrow 0}{[ \cos x+{\int }_{0}^{x}f(t)dt] }=1$。
步骤 3:应用洛必达法则
由于 $\lim _{x\rightarrow 0}{[ \cos x+{\int }_{0}^{x}f(t)dt] }=1$,因此原极限可以写成 $\lim _{x\rightarrow 0}{[1+{\int }_{0}^{x}f(t)dt-\sin x] }^{\dfrac {1}{{x}^{2}}}$。令 $g(x)={\int }_{0}^{x}f(t)dt-\sin x$,则原极限可以写成 $\lim _{x\rightarrow 0}{(1+g(x))}^{\dfrac {1}{{x}^{2}}}$。应用洛必达法则,有 $\lim _{x\rightarrow 0}{(1+g(x))}^{\dfrac {1}{{x}^{2}}}=\lim _{x\rightarrow 0}{e}^{\dfrac {g(x)}{{x}^{2}}}$。由于 $\lim _{x\rightarrow 0}\dfrac {g(x)}{{x}^{2}}=\lim _{x\rightarrow 0}\dfrac {f(x)-\cos x}{2x}=\lim _{x\rightarrow 0}\dfrac {f(x)}{2}=\dfrac {f'(0)}{2}=1$,因此原极限为 $\lim _{x\rightarrow 0}{e}^{\dfrac {g(x)}{{x}^{2}}}=e$。
曲线 y=f(x) 在点 (0,0) 处的切线过点 (1,2),因此切线方程为 y=2x。由此可知 f(0)=0,f'(0)=2。
步骤 2:计算极限
考虑极限 $\lim _{x\rightarrow 0}{[ \cos x+{\int }_{0}^{x}f(t)dt] }^{\dfrac {1}{{x}^{2}}}$,首先计算 $\cos x+{\int }_{0}^{x}f(t)dt$ 在 x 趋近于 0 时的极限。
由于 $\lim _{x\rightarrow 0}\cos x=1$,且 $\lim _{x\rightarrow 0}{\int }_{0}^{x}f(t)dt=0$,因此 $\lim _{x\rightarrow 0}{[ \cos x+{\int }_{0}^{x}f(t)dt] }=1$。
步骤 3:应用洛必达法则
由于 $\lim _{x\rightarrow 0}{[ \cos x+{\int }_{0}^{x}f(t)dt] }=1$,因此原极限可以写成 $\lim _{x\rightarrow 0}{[1+{\int }_{0}^{x}f(t)dt-\sin x] }^{\dfrac {1}{{x}^{2}}}$。令 $g(x)={\int }_{0}^{x}f(t)dt-\sin x$,则原极限可以写成 $\lim _{x\rightarrow 0}{(1+g(x))}^{\dfrac {1}{{x}^{2}}}$。应用洛必达法则,有 $\lim _{x\rightarrow 0}{(1+g(x))}^{\dfrac {1}{{x}^{2}}}=\lim _{x\rightarrow 0}{e}^{\dfrac {g(x)}{{x}^{2}}}$。由于 $\lim _{x\rightarrow 0}\dfrac {g(x)}{{x}^{2}}=\lim _{x\rightarrow 0}\dfrac {f(x)-\cos x}{2x}=\lim _{x\rightarrow 0}\dfrac {f(x)}{2}=\dfrac {f'(0)}{2}=1$,因此原极限为 $\lim _{x\rightarrow 0}{e}^{\dfrac {g(x)}{{x}^{2}}}=e$。