题目
求微分方程''+y'-2y=4-2x的通解
求微分方程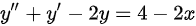
的通解
题目解答
答案
∵微分方程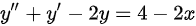
∴齐次方程为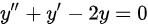
特征方程为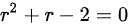
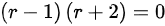
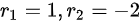
∴齐次方程的通解为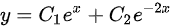
又∵微分方程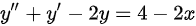
右边形式为一次方程，且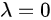
不是特征方程的根
∴设特解形式为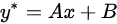
代入微分方程可得
∴
∴
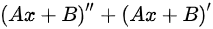
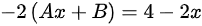
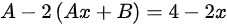
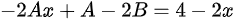
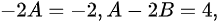
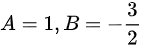
∴特解为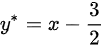
∴微分方程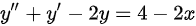的通解为
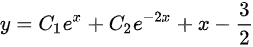
解析
步骤 1：求解齐次方程的通解
首先，我们求解齐次方程y''+y'-2y=0的通解。为此，我们先求解特征方程$r^2 + r - 2 = 0$。解得$r_1 = 1$和$r_2 = -2$。因此，齐次方程的通解为$y = C_1e^{x} + C_2e^{-2x}$，其中$C_1$和$C_2$是任意常数。
步骤 2：求解非齐次方程的特解
接下来，我们求解非齐次方程y''+y'-2y=4-2x的特解。由于非齐次项为一次多项式，且$\lambda = 0$不是特征方程的根，我们设特解形式为$y = Ax + B$。将$y = Ax + B$代入原方程，得到$A - 2(Ax + B) = 4 - 2x$。通过比较系数，我们得到$-2A = -2$和$A - 2B = 4$。解得$A = 1$和$B = -\frac{3}{2}$。因此，特解为$y^* = x - \frac{3}{2}$。
步骤 3：求解非齐次方程的通解
最后，非齐次方程的通解为齐次方程的通解加上特解，即$y = C_1e^{x} + C_2e^{-2x} + x - \frac{3}{2}$。
首先，我们求解齐次方程y''+y'-2y=0的通解。为此，我们先求解特征方程$r^2 + r - 2 = 0$。解得$r_1 = 1$和$r_2 = -2$。因此，齐次方程的通解为$y = C_1e^{x} + C_2e^{-2x}$，其中$C_1$和$C_2$是任意常数。
步骤 2：求解非齐次方程的特解
接下来，我们求解非齐次方程y''+y'-2y=4-2x的特解。由于非齐次项为一次多项式，且$\lambda = 0$不是特征方程的根，我们设特解形式为$y = Ax + B$。将$y = Ax + B$代入原方程，得到$A - 2(Ax + B) = 4 - 2x$。通过比较系数，我们得到$-2A = -2$和$A - 2B = 4$。解得$A = 1$和$B = -\frac{3}{2}$。因此，特解为$y^* = x - \frac{3}{2}$。
步骤 3：求解非齐次方程的通解
最后，非齐次方程的通解为齐次方程的通解加上特解，即$y = C_1e^{x} + C_2e^{-2x} + x - \frac{3}{2}$。