题目
求微分方程 ^m+6(y)^n+(9+(a)^2)y'=1 的通解,其中常 数 gt 0.
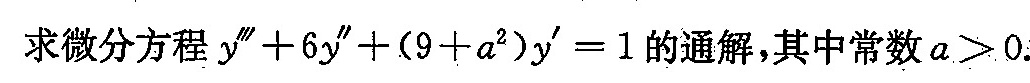
题目解答
答案

解析
步骤 1:求解齐次方程的特征方程
给定微分方程为 ${y}^{m}+6{y}^{n}+(9+{a}^{2})y'=1$,其中 $m=3$,$n=2$。首先,我们考虑对应的齐次方程 ${y}^{m}+6{y}^{n}+(9+{a}^{2})y'=0$。其特征方程为 ${r}^{3}+6{r}^{2}+(9+{a}^{2})r=0$。解此方程,我们得到特征根 ${r}_{1}=0$,${r}_{2}=-3+ai$,${r}_{3}=-3-ai$。
步骤 2:求解齐次方程的通解
根据特征根,齐次方程的通解为 $\overline {y}={C}_{1}+{e}^{-3x}({C}_{2}\cos ax+{C}_{3}\sin ax)$。
步骤 3:求解非齐次方程的特解
由于 $a=0$ 为单根,因此可设非齐次方程的特解为 ${y}^{*}=Ax$。将 ${y}^{*}=Ax$ 代入原方程 ${y}^{m}+6{y}^{n}+(9+{a}^{2})y'=1$,得到 $A= \dfrac {1}{9+{a}^{2}}$。因此,特解为 ${y}^{*}=\dfrac {1}{9+{a}^{2}}x$。
步骤 4:求解原方程的通解
原方程的通解为 $y=\overline {y}+{y}^{*}={C}_{1}+{e}^{-3x}({C}_{2}\cos ax+{C}_{3}\sin ax)+\dfrac {1}{9+{a}^{2}}x$。
给定微分方程为 ${y}^{m}+6{y}^{n}+(9+{a}^{2})y'=1$,其中 $m=3$,$n=2$。首先,我们考虑对应的齐次方程 ${y}^{m}+6{y}^{n}+(9+{a}^{2})y'=0$。其特征方程为 ${r}^{3}+6{r}^{2}+(9+{a}^{2})r=0$。解此方程,我们得到特征根 ${r}_{1}=0$,${r}_{2}=-3+ai$,${r}_{3}=-3-ai$。
步骤 2:求解齐次方程的通解
根据特征根,齐次方程的通解为 $\overline {y}={C}_{1}+{e}^{-3x}({C}_{2}\cos ax+{C}_{3}\sin ax)$。
步骤 3:求解非齐次方程的特解
由于 $a=0$ 为单根,因此可设非齐次方程的特解为 ${y}^{*}=Ax$。将 ${y}^{*}=Ax$ 代入原方程 ${y}^{m}+6{y}^{n}+(9+{a}^{2})y'=1$,得到 $A= \dfrac {1}{9+{a}^{2}}$。因此,特解为 ${y}^{*}=\dfrac {1}{9+{a}^{2}}x$。
步骤 4:求解原方程的通解
原方程的通解为 $y=\overline {y}+{y}^{*}={C}_{1}+{e}^{-3x}({C}_{2}\cos ax+{C}_{3}\sin ax)+\dfrac {1}{9+{a}^{2}}x$。