题目
求曲线 xy = 2 与直线 x = 2 , x = 2 , x = 4 及 y=0 所围成的图形分别绕 x 轴 y 轴 旋转所得旋转体的体积
求曲线 xy = 2 与直线 x = 2 , x = 2 , x = 4 及 y=0 所围成的图形分别绕 x 轴 y 轴 旋转所得旋转体的体积
题目解答
答案
解题如下
解:
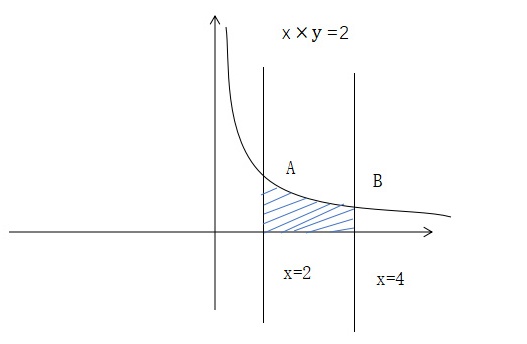
交点A(2,1),交点B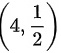
f(x)绕x轴在区间[2,4]旋转一周所得的体积如下
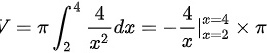
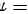
f(x)绕y轴在区间[2,4]旋转一周所得的体积如下
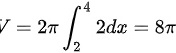
解析
步骤 1:确定曲线与直线的交点
曲线 $xy = 2$ 与直线 $x = 2$ 的交点为 $(2, 1)$,与直线 $x = 4$ 的交点为 $(4, \frac{1}{2})$。因此,所围成的图形在 $x$ 轴上的区间为 $[2, 4]$。
步骤 2:计算绕 $x$ 轴旋转的体积
绕 $x$ 轴旋转的体积可以通过计算旋转体的横截面面积的积分来得到。横截面面积为 $\pi y^2$,其中 $y = \frac{2}{x}$。因此,体积 $V_x$ 为:
$$
V_x = \pi \int_{2}^{4} \left(\frac{2}{x}\right)^2 dx = \pi \int_{2}^{4} \frac{4}{x^2} dx
$$
计算积分:
$$
V_x = \pi \left[-\frac{4}{x}\right]_{2}^{4} = \pi \left(-\frac{4}{4} + \frac{4}{2}\right) = \pi \left(-1 + 2\right) = \pi
$$
步骤 3:计算绕 $y$ 轴旋转的体积
绕 $y$ 轴旋转的体积可以通过计算旋转体的横截面面积的积分来得到。横截面面积为 $\pi x^2$,其中 $x = \frac{2}{y}$。因此,体积 $V_y$ 为:
$$
V_y = \pi \int_{\frac{1}{2}}^{1} \left(\frac{2}{y}\right)^2 dy = \pi \int_{\frac{1}{2}}^{1} \frac{4}{y^2} dy
$$
计算积分:
$$
V_y = \pi \left[-\frac{4}{y}\right]_{\frac{1}{2}}^{1} = \pi \left(-\frac{4}{1} + \frac{4}{\frac{1}{2}}\right) = \pi \left(-4 + 8\right) = 4\pi
$$
曲线 $xy = 2$ 与直线 $x = 2$ 的交点为 $(2, 1)$,与直线 $x = 4$ 的交点为 $(4, \frac{1}{2})$。因此,所围成的图形在 $x$ 轴上的区间为 $[2, 4]$。
步骤 2:计算绕 $x$ 轴旋转的体积
绕 $x$ 轴旋转的体积可以通过计算旋转体的横截面面积的积分来得到。横截面面积为 $\pi y^2$,其中 $y = \frac{2}{x}$。因此,体积 $V_x$ 为:
$$
V_x = \pi \int_{2}^{4} \left(\frac{2}{x}\right)^2 dx = \pi \int_{2}^{4} \frac{4}{x^2} dx
$$
计算积分:
$$
V_x = \pi \left[-\frac{4}{x}\right]_{2}^{4} = \pi \left(-\frac{4}{4} + \frac{4}{2}\right) = \pi \left(-1 + 2\right) = \pi
$$
步骤 3:计算绕 $y$ 轴旋转的体积
绕 $y$ 轴旋转的体积可以通过计算旋转体的横截面面积的积分来得到。横截面面积为 $\pi x^2$,其中 $x = \frac{2}{y}$。因此,体积 $V_y$ 为:
$$
V_y = \pi \int_{\frac{1}{2}}^{1} \left(\frac{2}{y}\right)^2 dy = \pi \int_{\frac{1}{2}}^{1} \frac{4}{y^2} dy
$$
计算积分:
$$
V_y = \pi \left[-\frac{4}{y}\right]_{\frac{1}{2}}^{1} = \pi \left(-\frac{4}{1} + \frac{4}{\frac{1}{2}}\right) = \pi \left(-4 + 8\right) = 4\pi
$$