题目
(5)设 (x,y)=ln (x+dfrac (y)(2x)) ,则 _(y)'(1,0)= () .-|||-(A)1 (B) dfrac (1)(2) (C)2 (D)0
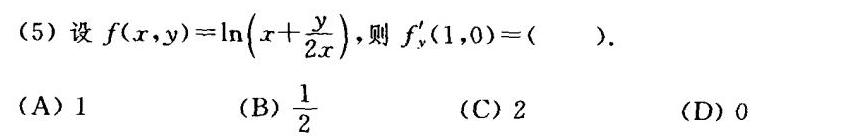
题目解答
答案
解析
步骤 1:求偏导数
首先,我们需要对函数 $f(x,y)=\ln (x+\dfrac {y}{2x})$ 关于变量 $y$ 求偏导数。根据链式法则,我们有:
$$
{f}_{y}'(x,y) = \frac{1}{x+\frac{y}{2x}} \cdot \frac{\partial}{\partial y} \left(x+\frac{y}{2x}\right)
$$
步骤 2:计算偏导数
计算偏导数 $\frac{\partial}{\partial y} \left(x+\frac{y}{2x}\right)$,我们得到:
$$
\frac{\partial}{\partial y} \left(x+\frac{y}{2x}\right) = \frac{1}{2x}
$$
因此,偏导数 ${f}_{y}'(x,y)$ 可以表示为:
$$
{f}_{y}'(x,y) = \frac{1}{x+\frac{y}{2x}} \cdot \frac{1}{2x} = \frac{1}{2x(x+\frac{y}{2x})}
$$
步骤 3:代入点 (1,0)
将点 (1,0) 代入偏导数 ${f}_{y}'(x,y)$,我们得到:
$$
{f}_{y}'(1,0) = \frac{1}{2 \cdot 1 \cdot (1+\frac{0}{2 \cdot 1})} = \frac{1}{2}
$$
首先,我们需要对函数 $f(x,y)=\ln (x+\dfrac {y}{2x})$ 关于变量 $y$ 求偏导数。根据链式法则,我们有:
$$
{f}_{y}'(x,y) = \frac{1}{x+\frac{y}{2x}} \cdot \frac{\partial}{\partial y} \left(x+\frac{y}{2x}\right)
$$
步骤 2:计算偏导数
计算偏导数 $\frac{\partial}{\partial y} \left(x+\frac{y}{2x}\right)$,我们得到:
$$
\frac{\partial}{\partial y} \left(x+\frac{y}{2x}\right) = \frac{1}{2x}
$$
因此,偏导数 ${f}_{y}'(x,y)$ 可以表示为:
$$
{f}_{y}'(x,y) = \frac{1}{x+\frac{y}{2x}} \cdot \frac{1}{2x} = \frac{1}{2x(x+\frac{y}{2x})}
$$
步骤 3:代入点 (1,0)
将点 (1,0) 代入偏导数 ${f}_{y}'(x,y)$,我们得到:
$$
{f}_{y}'(1,0) = \frac{1}{2 \cdot 1 \cdot (1+\frac{0}{2 \cdot 1})} = \frac{1}{2}
$$