题目
设曲线的极坐标方程为 =(e)^atheta (agt 0), 则该曲线上相应于θ从0变到2π的-|||-一段弧与极轴所围成的图形的面积为 __
题目解答
答案
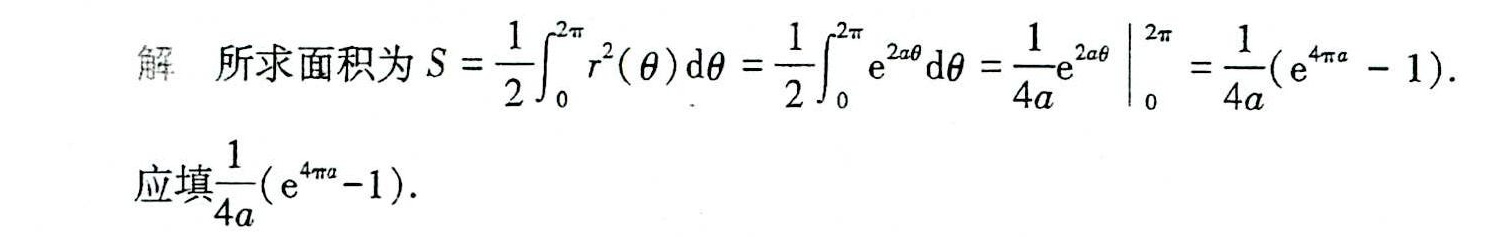
解析
考查要点:本题主要考查极坐标系下平面图形面积的计算方法,需要掌握极坐标方程对应的面积积分公式,并能正确进行定积分运算。
解题核心思路:
- 极坐标面积公式:极坐标下,由曲线$r=r(\theta)$从$\theta_1$到$\theta_2$围成的面积公式为$S=\dfrac{1}{2}\int_{\theta_1}^{\theta_2} r^2 \, d\theta$。
- 代入方程:将题目中的$r=e^{a\theta}$代入公式,转化为对$\theta$的定积分。
- 积分计算:通过指数函数的积分规则求解定积分,并代入上下限$\theta=0$到$\theta=2\pi$。
破题关键点:
- 正确应用面积公式,注意公式中是$r^2$而非$r$。
- 积分变量替换:将$e^{a\theta}$平方后得到$e^{2a\theta}$,积分时需注意系数处理。
根据极坐标面积公式,所求面积为:
$S = \dfrac{1}{2} \int_{0}^{2\pi} \left( e^{a\theta} \right)^2 d\theta$
步骤1:化简被积函数
将$r^2$展开:
$\left( e^{a\theta} \right)^2 = e^{2a\theta}$
步骤2:计算定积分
积分$\int e^{2a\theta} d\theta$的原函数为$\dfrac{1}{2a} e^{2a\theta}$,代入上下限:
$\int_{0}^{2\pi} e^{2a\theta} d\theta = \left. \dfrac{1}{2a} e^{2a\theta} \right|_{0}^{2\pi} = \dfrac{1}{2a} \left( e^{4\pi a} - 1 \right)$
步骤3:代入面积公式
将积分结果乘以$\dfrac{1}{2}$:
$S = \dfrac{1}{2} \cdot \dfrac{1}{2a} \left( e^{4\pi a} - 1 \right) = \dfrac{1}{4a} \left( e^{4\pi a} - 1 \right)$