题目
下列各题中 ,函数 f(x)和g(x)是否相同?为什么?-|||-(1) (x)=lg (x)^2, (x)=2lg x;-|||-(2) (x)=x, (x)=sqrt ({x)^2};-|||-(3) (x)=sqrt [3]({x)^4-(x)^3}, (x)=xsqrt [3](x-1);-|||-(4) (x)=1, (x)=(sec )^2x-(tan )^2x.
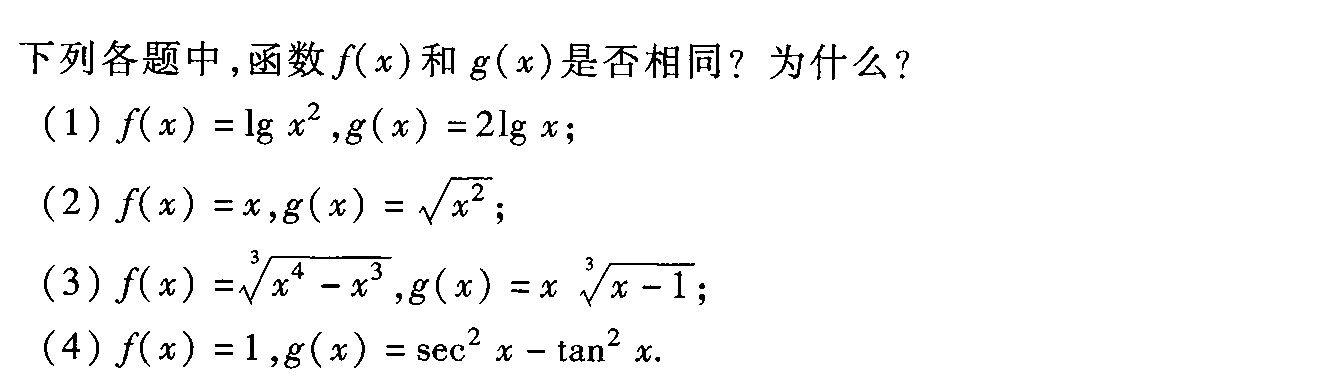
题目解答
答案

解析
判断两个函数是否相同,需同时满足两个条件:
- 定义域相同;
- 对应法则相同(即对定义域内的任意$x$,$f(x)=g(x)$)。
关键思路:
- 定义域分析:分别求出两个函数的定义域,若不同则直接排除;
- 对应法则分析:若定义域相同,需验证是否对所有$x$有$f(x)=g(x)$,注意化简时可能隐藏的条件限制。
第(1)题
$f(x)=\lg x^2$与$g(x)=2\lg x$
- 定义域分析:
- $f(x)$中$\lg x^2$要求$x^2>0$,即$x \neq 0$,定义域为$(-\infty,0) \cup (0,+\infty)$;
- $g(x)$中$\lg x$要求$x>0$,定义域为$(0,+\infty)$;
- 定义域不同,函数不同。
第(2)题
$f(x)=x$与$g(x)=\sqrt{x^2}$
- 对应法则分析:
- $g(x)=\sqrt{x^2}=|x|=\begin{cases}x, & x \geq 0 \\ -x, & x < 0\end{cases}$;
- 当$x<0$时,$f(x)=x \neq g(x)=-x$;
- 对应法则不同,函数不同。
第(3)题
$f(x)=\sqrt[3]{x^4-x^3}$与$g(x)=x\sqrt[3]{x-1}$
- 化简表达式:
- $f(x)=\sqrt[3]{x^3(x-1)}=x\sqrt[3]{x-1}=g(x)$;
- 定义域分析:
- 三次根号下表达式对任意实数有意义,定义域均为$\mathbb{R}$;
- 定义域和对应法则均相同,函数相同。
第(4)题
$f(x)=1$与$g(x)=\sec^2 x - \tan^2 x$
- 恒等变形:
- 利用三角恒等式$\sec^2 x - \tan^2 x = 1$,故$g(x)=1$;
- 定义域分析:
- $f(x)$定义域为$\mathbb{R}$;
- $g(x)$中$\sec x$要求$\cos x \neq 0$,即$x \neq \frac{\pi}{2} + k\pi$($k$为整数);
- 定义域不同,函数不同。