题目
2.求下列极限:-|||-(1) lim _(xarrow 0)dfrac ({x)^2-1}(3{x)^2-x-2}

题目解答
答案
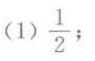
解析
步骤 1:因式分解分子和分母
分子 ${x}^{2}-1$ 可以因式分解为 $(x-1)(x+1)$,分母 $3{x}^{2}-x-2$ 可以因式分解为 $(3x+2)(x-1)$。
步骤 2:简化表达式
将因式分解后的分子和分母代入原式,得到 $\lim _{x\rightarrow 0}\dfrac {(x-1)(x+1)}{(3x+2)(x-1)}$。由于 $x\rightarrow 0$,$x-1$ 不为零,可以约去分子和分母中的 $(x-1)$,得到 $\lim _{x\rightarrow 0}\dfrac {x+1}{3x+2}$。
步骤 3:计算极限
将 $x=0$ 代入简化后的表达式,得到 $\dfrac {0+1}{3\cdot 0+2} = \dfrac {1}{2}$。
分子 ${x}^{2}-1$ 可以因式分解为 $(x-1)(x+1)$,分母 $3{x}^{2}-x-2$ 可以因式分解为 $(3x+2)(x-1)$。
步骤 2:简化表达式
将因式分解后的分子和分母代入原式,得到 $\lim _{x\rightarrow 0}\dfrac {(x-1)(x+1)}{(3x+2)(x-1)}$。由于 $x\rightarrow 0$,$x-1$ 不为零,可以约去分子和分母中的 $(x-1)$,得到 $\lim _{x\rightarrow 0}\dfrac {x+1}{3x+2}$。
步骤 3:计算极限
将 $x=0$ 代入简化后的表达式,得到 $\dfrac {0+1}{3\cdot 0+2} = \dfrac {1}{2}$。