一、计算下列极限。9.lim _(xarrow infty )(cos dfrac (x)(2)cos dfrac (x)(4)cos dfrac (x)(8)... cos dfrac (x)({2)^n})(提示:lim _(xarrow infty )(cos dfrac (x)(2)cos dfrac (x)(4)cos dfrac (x)(8)... cos dfrac (x)({2)^n}))
一、计算下列极限。
9.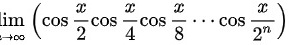 (提示:
(提示: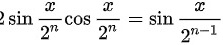 )
)
题目解答
答案
由题可知,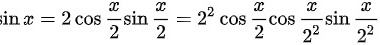 ,又等于
,又等于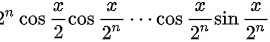 ,所以,
,所以,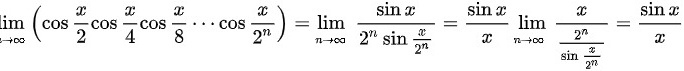 ,所以
,所以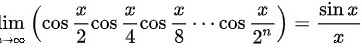 。
。
解析
考查要点:本题主要考查利用三角恒等式化简无限乘积,并结合极限求解的方法。关键在于递推应用提示中的恒等式,将余弦乘积转化为正弦函数表达式,进而分析极限。
解题核心思路:
- 利用提示中的恒等式,通过递推将余弦乘积转化为正弦函数的比值形式。
- 分析极限形式,当$x \rightarrow \infty$时,结合无穷乘积的特性,化简表达式。
- 应用等价无穷小替换,将极限转化为基本形式求解。
破题关键点:
- 递推应用恒等式:每次应用提示中的等式,逐步消去余弦项,最终得到关于$\sin x$的表达式。
- 无穷乘积的极限处理:当项数无限增加时,乘积中的分母项可近似为线性函数,从而简化极限计算。
步骤1:递推应用提示中的恒等式
根据提示:
$2\sin\frac{x}{2^n}\cos\frac{x}{2^n} = \sin\frac{x}{2^{n-1}}$
对乘积$\cos\frac{x}{2}\cos\frac{x}{4}\cdots\cos\frac{x}{2^n}$进行递推:
$\begin{aligned}\sin x &= 2\sin\frac{x}{2}\cos\frac{x}{2} \\&= 2^2\sin\frac{x}{4}\cos\frac{x}{4}\cos\frac{x}{2} \\&= \cdots \\&= 2^n\sin\frac{x}{2^n}\cos\frac{x}{2}\cos\frac{x}{4}\cdots\cos\frac{x}{2^{n-1}}.\end{aligned}$
因此,乘积可表示为:
$\cos\frac{x}{2}\cos\frac{x}{4}\cdots\cos\frac{x}{2^n} = \frac{\sin x}{2^n \sin\frac{x}{2^n}}.$
步骤2:分析极限形式
当$x \rightarrow \infty$时,若$n$固定,则$\frac{x}{2^n} \rightarrow \infty$,此时$\sin\frac{x}{2^n}$振荡无极限。但若乘积为无限乘积(即$n \rightarrow \infty$),则$\frac{x}{2^n} \rightarrow 0$,可应用等价无穷小替换:
$\sin\frac{x}{2^n} \approx \frac{x}{2^n}.$
代入表达式得:
$\cos\frac{x}{2}\cos\frac{x}{4}\cdots\cos\frac{x}{2^n} \approx \frac{\sin x}{2^n \cdot \frac{x}{2^n}} = \frac{\sin x}{x}.$
步骤3:求极限
当$x \rightarrow \infty$时,$\frac{\sin x}{x}$的极限为$0$(因$|\sin x| \leq 1$,分母趋于无穷大)。