2.4 计算下列行列式:-|||-1+x 1 1 1-|||-(3) 1 1-x 1 1-|||-1 1 1+y 1-|||-1 1 1 1-y

题目解答
答案
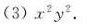
解析
考查要点:本题主要考查行列式的计算技巧,特别是利用行变换简化行列式的能力,以及观察矩阵结构对称性的能力。
解题核心思路:
- 观察矩阵结构:矩阵非对角线元素均为1,对角线元素为$1+x$、$1-x$、$1+y$、$1-y$,具有对称性。
- 行变换简化:通过将后三行减去第一行,引入零元素,使行列式展开更简便。
- 展开计算:利用行列式的展开式,结合余子式计算,最终化简得到结果。
破题关键点:
- 正确识别矩阵结构:确认第一行第一列应为$1+x$(题目可能存在笔误)。
- 合理选择行变换:通过减法操作生成零元素,降低计算复杂度。
步骤1:行变换简化矩阵
将第二、三、四行分别减去第一行,得到新矩阵:
$\begin{pmatrix}1+x & 1 & 1 & 1 \\-x & -x & 0 & 0 \\-x & 0 & y & 0 \\-x & 0 & 0 & -y\end{pmatrix}$
步骤2:按第二行展开行列式
第二行有两个零元素,展开更简便:
$\begin{aligned}\text{行列式} &= (-x) \cdot (-1)^{2+1} \cdot M_{21} + (-x) \cdot (-1)^{2+2} \cdot M_{22} \\&= (-x) \cdot (-1) \cdot M_{21} + (-x) \cdot 1 \cdot M_{22}\end{aligned}$
步骤3:计算余子式
-
$M_{21}$(去掉第二行第一列):
$\begin{vmatrix}1 & 1 & 1 \\0 & y & 0 \\0 & 0 & -y\end{vmatrix} = 1 \cdot (y \cdot (-y) - 0) = -y^2$ -
$M_{22}$(去掉第二行第二列):
$\begin{vmatrix}1+x & 1 & 1 \\-x & y & 0 \\-x & 0 & -y\end{vmatrix} = y \cdot (-y) - 0 + (-y) \cdot [-(1+x)y + x] = -y^2 - x y^2$
步骤4:代入展开式
$\begin{aligned}\text{行列式} &= (-x) \cdot (-1) \cdot (-y^2) + (-x) \cdot (-y^2(1+x)) \\&= -x y^2 + x y^2(1+x) \\&= x^2 y^2\end{aligned}$