题目
求曲线 =2t, =(t)^2, =dfrac (2)(3)(t)^3 上对应于=2t, =(t)^2, =dfrac (2)(3)(t)^3 的点处的切线及法平面方程。
求曲线 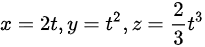 上对应于
上对应于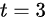 的点处的切线及法平面方程。
的点处的切线及法平面方程。
题目解答
答案
因为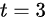 时,
时, 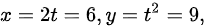
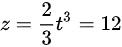 ,
,
所以,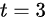 对应曲线上的点
对应曲线上的点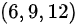 。
。
曲线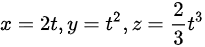 的切向量为
的切向量为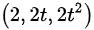 ,
,
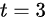 时,切向量
时,切向量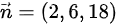 。
。
由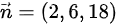 和点
和点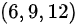 ,得到切线方程
,得到切线方程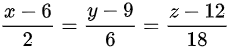 ,法平面
,法平面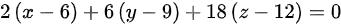 ,整理得到切线方程
,整理得到切线方程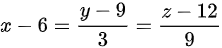 ,法平面
,法平面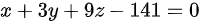 。
。
综上,切线方程为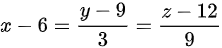 ,法平面为
,法平面为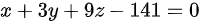 。
。
解析
步骤 1:确定曲线上的点
当t=3时,代入曲线方程x=2t, $y={t}^{2}$, $z=\dfrac {2}{3}{t}^{3}$,得到x=6, y=9, z=12。因此,t=3对应曲线上的点(6,9,12)。
步骤 2:计算切向量
曲线的切向量由参数t的导数确定。对x=2t, $y={t}^{2}$, $z=\dfrac {2}{3}{t}^{3}$分别求导,得到切向量(2,2t,2t^2)。当t=3时,切向量为(2,6,18)。
步骤 3:确定切线方程
由切向量(2,6,18)和点(6,9,12),可以得到切线方程$\dfrac {x-6}{2}=\dfrac {y-9}{6}=\dfrac {z-12}{18}$。简化得到切线方程$x-6=\dfrac {y-9}{3}=\dfrac {z-12}{9}$。
步骤 4:确定法平面方程
由切向量(2,6,18)和点(6,9,12),可以得到法平面方程2(x-6)+6(y-9)+18(z-12)=0。简化得到法平面方程x+3y+9z-141=0。
当t=3时,代入曲线方程x=2t, $y={t}^{2}$, $z=\dfrac {2}{3}{t}^{3}$,得到x=6, y=9, z=12。因此,t=3对应曲线上的点(6,9,12)。
步骤 2:计算切向量
曲线的切向量由参数t的导数确定。对x=2t, $y={t}^{2}$, $z=\dfrac {2}{3}{t}^{3}$分别求导,得到切向量(2,2t,2t^2)。当t=3时,切向量为(2,6,18)。
步骤 3:确定切线方程
由切向量(2,6,18)和点(6,9,12),可以得到切线方程$\dfrac {x-6}{2}=\dfrac {y-9}{6}=\dfrac {z-12}{18}$。简化得到切线方程$x-6=\dfrac {y-9}{3}=\dfrac {z-12}{9}$。
步骤 4:确定法平面方程
由切向量(2,6,18)和点(6,9,12),可以得到法平面方程2(x-6)+6(y-9)+18(z-12)=0。简化得到法平面方程x+3y+9z-141=0。