题目
设矩阵满足则_______________ .
设矩阵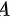
满足
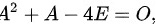则
_______________ .
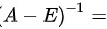题目解答
答案
∵
∴
∴
∴
∴
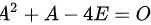
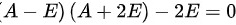
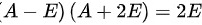
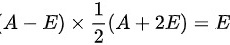
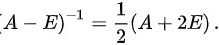
因此:该题填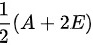
。
解析
步骤 1：利用已知条件
已知矩阵$A$满足${A}^{2}+A-4E=0$，其中$E$是单位矩阵。我们需要找到${(A-E)}^{-1}$的表达式。
步骤 2：构造等式
为了找到${(A-E)}^{-1}$，我们首先构造一个等式，使得$(A-E)$乘以某个矩阵等于单位矩阵$E$。根据已知条件，我们有${A}^{2}+A-4E=0$，可以变形为${A}^{2}+A=4E$。
步骤 3：变形等式
将${A}^{2}+A=4E$变形为$(A-E)(A+2E)=2E$。这是因为$(A-E)(A+2E)=A^2+2A-A-2E=A^2+A-2E=4E-2E=2E$。
步骤 4：求逆矩阵
由$(A-E)(A+2E)=2E$，两边同时乘以$\dfrac{1}{2}$，得到$(A-E)\times \dfrac{1}{2}(A+2E)=E$。这表明$\dfrac{1}{2}(A+2E)$是$(A-E)$的逆矩阵。
已知矩阵$A$满足${A}^{2}+A-4E=0$，其中$E$是单位矩阵。我们需要找到${(A-E)}^{-1}$的表达式。
步骤 2：构造等式
为了找到${(A-E)}^{-1}$，我们首先构造一个等式，使得$(A-E)$乘以某个矩阵等于单位矩阵$E$。根据已知条件，我们有${A}^{2}+A-4E=0$，可以变形为${A}^{2}+A=4E$。
步骤 3：变形等式
将${A}^{2}+A=4E$变形为$(A-E)(A+2E)=2E$。这是因为$(A-E)(A+2E)=A^2+2A-A-2E=A^2+A-2E=4E-2E=2E$。
步骤 4：求逆矩阵
由$(A-E)(A+2E)=2E$，两边同时乘以$\dfrac{1}{2}$，得到$(A-E)\times \dfrac{1}{2}(A+2E)=E$。这表明$\dfrac{1}{2}(A+2E)$是$(A-E)$的逆矩阵。