题目
矩阵A为n阶方阵n > 2 则其伴随阵 A *的秩可能为A 1 B nC n-1D n-2E 0
矩阵A为n阶方阵n > 2 则其伴随阵 A *的秩可能为
A 1
B n
C n-1
D n-2
E 0
题目解答
答案
答案为:A,B,E
由已知和矩阵的秩和其伴随矩阵的秩有以下关系:
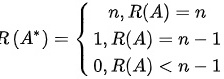
∴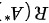 只有三种情况:n,1,0
只有三种情况:n,1,0
所以选择A,C,E
解析
考查要点:本题主要考查n阶方阵的伴随矩阵的秩与原矩阵秩之间的关系,需要掌握伴随矩阵秩的取值规律。
解题核心思路:
根据矩阵秩与伴随矩阵秩的对应关系:
- 当原矩阵秩$R(A)=n$时,伴随矩阵秩$R(A^*)=n$;
- 当原矩阵秩$R(A)=n-1$时,伴随矩阵秩$R(A^*)=1$;
- 当原矩阵秩$R(A) \leq n-2$时,伴随矩阵秩$R(A^*)=0$。
破题关键点:
- 明确伴随矩阵秩的取值仅与原矩阵秩是否达到$n$、$n-1$或更低直接相关。
- 排除选项中不符合上述规律的情况(如$n-1$或$n-2$)。
根据矩阵秩与伴随矩阵秩的关系:
$R(A^*) =
\begin{cases} n, & R(A) = n, \\1, & R(A) = n-1, \\0, & R(A) \leq n-2.\end{cases}$
具体分析:
-
当$R(A)=n$时:
原矩阵$A$可逆,此时$A^*$也可逆,故$R(A^*)=n$(对应选项B)。 -
当$R(A)=n-1$时:
$A$的所有$(n-1)$阶余子式不全为零,但所有$n$阶余子式(即行列式)为零,因此$A^*$的所有列(或行)成比例,秩为1(对应选项A)。 -
当$R(A) \leq n-2$时:
$A$的所有$(n-1)$阶余子式均为零,故$A^*$为零矩阵,秩为0(对应选项E)。
排除错误选项:
- 选项C($n-1$):伴随矩阵的秩不可能等于$n-1$。
- 选项D($n-2$):当$R(A)=n-2$时,$R(A^*)=0$,而非$n-2$。