题目
3.计算曲面积分 https:/img.zuoyebang.cc/zyb_249d34adfff889d5be31883dabf1e155.jpg=iint ((x)^3+(z)^3)dydz+((y)^3+(x)^2)dxdx+((z)^3+(y)^2)dxdy ,其中∑为 =sqrt (1-{x)^2-(y)^2}-|||-的上侧.
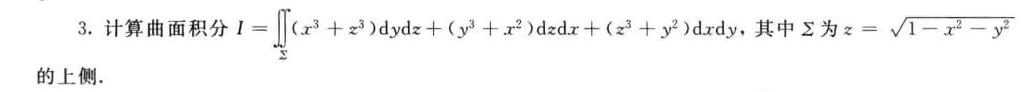
题目解答
答案

解析
步骤 1:确定积分区域
给定的曲面是 $z=\sqrt{1-x^2-y^2}$,这是一个半径为1的上半球面。积分区域是这个球面的上侧,即 $z\geq0$。
步骤 2:应用高斯定理
高斯定理(散度定理)表明,对于一个闭合曲面S,其上的向量场F的通量等于该向量场在闭合曲面所围成的体积V内的散度的积分。即:
$$\iint_{S} \mathbf{F} \cdot d\mathbf{S} = \iiint_{V} \nabla \cdot \mathbf{F} \, dV$$
其中,$\mathbf{F} = (x^3+z^3, y^3+x^2, z^3+y^2)$,$\nabla \cdot \mathbf{F} = \frac{\partial}{\partial x}(x^3+z^3) + \frac{\partial}{\partial y}(y^3+x^2) + \frac{\partial}{\partial z}(z^3+y^2)$。
步骤 3:计算散度
计算向量场F的散度:
$$\nabla \cdot \mathbf{F} = 3x^2 + 3y^2 + 3z^2$$
由于积分区域是半径为1的球体,我们可以将散度积分转换为球坐标下的积分:
$$\iiint_{V} (3x^2 + 3y^2 + 3z^2) \, dV = 3\iiint_{V} (x^2 + y^2 + z^2) \, dV$$
在球坐标系中,$x^2 + y^2 + z^2 = r^2$,$dV = r^2 \sin\theta \, dr \, d\theta \, d\phi$,积分范围为$0 \leq r \leq 1$,$0 \leq \theta \leq \pi$,$0 \leq \phi \leq 2\pi$。因此,积分变为:
$$3\int_{0}^{2\pi} \int_{0}^{\pi} \int_{0}^{1} r^4 \sin\theta \, dr \, d\theta \, d\phi$$
步骤 4:计算积分
计算上述积分:
$$3\int_{0}^{2\pi} \int_{0}^{\pi} \int_{0}^{1} r^4 \sin\theta \, dr \, d\theta \, d\phi = 3\int_{0}^{2\pi} d\phi \int_{0}^{\pi} \sin\theta \, d\theta \int_{0}^{1} r^4 \, dr$$
$$= 3\cdot 2\pi \cdot 2 \cdot \frac{1}{5} = \frac{24\pi}{5}$$
步骤 5:考虑补面
由于原积分区域是上半球面,我们需要考虑补面,即 $z=0$ 平面上的圆盘,其面积为 $\pi$。补面的积分是:
$$\iint_{z=0} (y^2) \, dxdy = \pi$$
因此,总积分是:
$$\frac{24\pi}{5} - \pi = \frac{19\pi}{5}$$
给定的曲面是 $z=\sqrt{1-x^2-y^2}$,这是一个半径为1的上半球面。积分区域是这个球面的上侧,即 $z\geq0$。
步骤 2:应用高斯定理
高斯定理(散度定理)表明,对于一个闭合曲面S,其上的向量场F的通量等于该向量场在闭合曲面所围成的体积V内的散度的积分。即:
$$\iint_{S} \mathbf{F} \cdot d\mathbf{S} = \iiint_{V} \nabla \cdot \mathbf{F} \, dV$$
其中,$\mathbf{F} = (x^3+z^3, y^3+x^2, z^3+y^2)$,$\nabla \cdot \mathbf{F} = \frac{\partial}{\partial x}(x^3+z^3) + \frac{\partial}{\partial y}(y^3+x^2) + \frac{\partial}{\partial z}(z^3+y^2)$。
步骤 3:计算散度
计算向量场F的散度:
$$\nabla \cdot \mathbf{F} = 3x^2 + 3y^2 + 3z^2$$
由于积分区域是半径为1的球体,我们可以将散度积分转换为球坐标下的积分:
$$\iiint_{V} (3x^2 + 3y^2 + 3z^2) \, dV = 3\iiint_{V} (x^2 + y^2 + z^2) \, dV$$
在球坐标系中,$x^2 + y^2 + z^2 = r^2$,$dV = r^2 \sin\theta \, dr \, d\theta \, d\phi$,积分范围为$0 \leq r \leq 1$,$0 \leq \theta \leq \pi$,$0 \leq \phi \leq 2\pi$。因此,积分变为:
$$3\int_{0}^{2\pi} \int_{0}^{\pi} \int_{0}^{1} r^4 \sin\theta \, dr \, d\theta \, d\phi$$
步骤 4:计算积分
计算上述积分:
$$3\int_{0}^{2\pi} \int_{0}^{\pi} \int_{0}^{1} r^4 \sin\theta \, dr \, d\theta \, d\phi = 3\int_{0}^{2\pi} d\phi \int_{0}^{\pi} \sin\theta \, d\theta \int_{0}^{1} r^4 \, dr$$
$$= 3\cdot 2\pi \cdot 2 \cdot \frac{1}{5} = \frac{24\pi}{5}$$
步骤 5:考虑补面
由于原积分区域是上半球面,我们需要考虑补面,即 $z=0$ 平面上的圆盘,其面积为 $\pi$。补面的积分是:
$$\iint_{z=0} (y^2) \, dxdy = \pi$$
因此,总积分是:
$$\frac{24\pi}{5} - \pi = \frac{19\pi}{5}$$