题目
3.已知 '(x)=(e)^-x ,且 f(0)=0 ,则 int f(-x)dx= ( ).()-|||-A. - -(e)^-x+x+C B. ^-x+x+c C. -(e)^x+x+c D. ^x+x+c
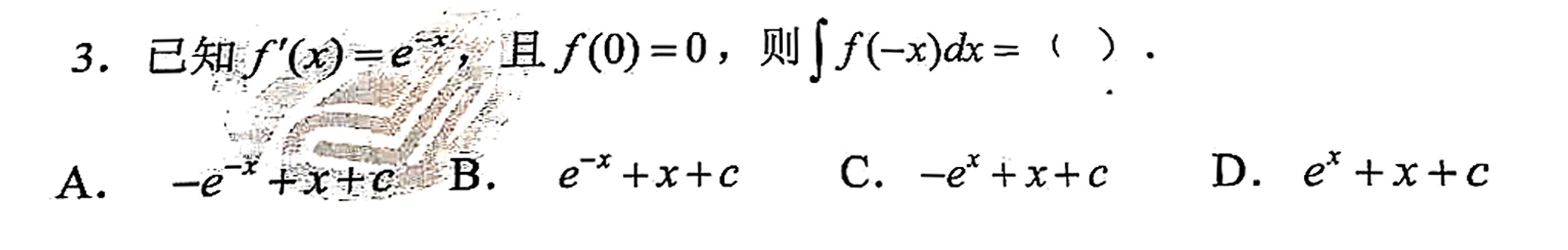
题目解答
答案

解析
步骤 1:求解 $f(x)$
已知 $f'(x) = e^{-x}$,对 $f'(x)$ 积分得到 $f(x)$。
$$
f(x) = \int e^{-x} dx = -e^{-x} + C
$$
步骤 2:确定常数 $C$
已知 $f(0) = 0$,代入 $f(x)$ 中求解 $C$。
$$
f(0) = -e^{-0} + C = 0
$$
$$
C = 1
$$
步骤 3:求解 $f(-x)$
将 $x$ 替换为 $-x$,得到 $f(-x)$。
$$
f(-x) = -e^{x} + 1
$$
步骤 4:求解 $\int f(-x) dx$
对 $f(-x)$ 积分。
$$
\int f(-x) dx = \int (-e^{x} + 1) dx = -e^{x} + x + C
$$
已知 $f'(x) = e^{-x}$,对 $f'(x)$ 积分得到 $f(x)$。
$$
f(x) = \int e^{-x} dx = -e^{-x} + C
$$
步骤 2:确定常数 $C$
已知 $f(0) = 0$,代入 $f(x)$ 中求解 $C$。
$$
f(0) = -e^{-0} + C = 0
$$
$$
C = 1
$$
步骤 3:求解 $f(-x)$
将 $x$ 替换为 $-x$,得到 $f(-x)$。
$$
f(-x) = -e^{x} + 1
$$
步骤 4:求解 $\int f(-x) dx$
对 $f(-x)$ 积分。
$$
\int f(-x) dx = \int (-e^{x} + 1) dx = -e^{x} + x + C
$$