题目
(2)设A是正交矩阵,则 |A|= __ 。

题目解答
答案
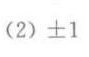
解析
步骤 1:定义正交矩阵
正交矩阵是指其转置等于其逆的方阵,即 $A^T = A^{-1}$。这意味着 $A$ 的列向量是标准正交的,即它们是单位向量且彼此正交。
步骤 2:计算行列式
对于正交矩阵 $A$,我们有 $A^T A = I$,其中 $I$ 是单位矩阵。行列式的性质之一是 $|A^T| = |A|$,因此 $|A^T A| = |A|^2 = |I| = 1$。由于 $|I| = 1$,我们得到 $|A|^2 = 1$。
步骤 3:求解行列式的值
从 $|A|^2 = 1$,我们可以得出 $|A| = \pm 1$。这是因为 $1$ 的平方根是 $\pm 1$。
正交矩阵是指其转置等于其逆的方阵,即 $A^T = A^{-1}$。这意味着 $A$ 的列向量是标准正交的,即它们是单位向量且彼此正交。
步骤 2:计算行列式
对于正交矩阵 $A$,我们有 $A^T A = I$,其中 $I$ 是单位矩阵。行列式的性质之一是 $|A^T| = |A|$,因此 $|A^T A| = |A|^2 = |I| = 1$。由于 $|I| = 1$,我们得到 $|A|^2 = 1$。
步骤 3:求解行列式的值
从 $|A|^2 = 1$,我们可以得出 $|A| = \pm 1$。这是因为 $1$ 的平方根是 $\pm 1$。