题目
9.计算下列定积分:-|||-(1) (int )_(0)^asqrt ({a)^2-(x)^2}dx(agt 0);

题目解答
答案
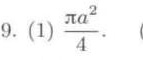
解析
步骤 1:确定积分的几何意义
积分 ${\int }_{0}^{a}\sqrt {{a}^{2}-{x}^{2}}dx$ 表示的是在区间 $[0, a]$ 上,函数 $y = \sqrt{a^2 - x^2}$ 的图形与 $x$ 轴围成的面积。由于 $y = \sqrt{a^2 - x^2}$ 是一个半圆的上半部分,因此这个积分实际上表示的是半径为 $a$ 的半圆的面积的一半。
步骤 2:计算半圆的面积
半圆的面积是 $\frac{1}{2} \pi a^2$,因此半圆的一半的面积是 $\frac{1}{4} \pi a^2$。
步骤 3:得出积分的值
根据步骤 2 的结果,积分 ${\int }_{0}^{a}\sqrt {{a}^{2}-{x}^{2}}dx$ 的值为 $\frac{1}{4} \pi a^2$。
积分 ${\int }_{0}^{a}\sqrt {{a}^{2}-{x}^{2}}dx$ 表示的是在区间 $[0, a]$ 上,函数 $y = \sqrt{a^2 - x^2}$ 的图形与 $x$ 轴围成的面积。由于 $y = \sqrt{a^2 - x^2}$ 是一个半圆的上半部分,因此这个积分实际上表示的是半径为 $a$ 的半圆的面积的一半。
步骤 2:计算半圆的面积
半圆的面积是 $\frac{1}{2} \pi a^2$,因此半圆的一半的面积是 $\frac{1}{4} \pi a^2$。
步骤 3:得出积分的值
根据步骤 2 的结果,积分 ${\int }_{0}^{a}\sqrt {{a}^{2}-{x}^{2}}dx$ 的值为 $\frac{1}{4} \pi a^2$。