题目
已知 L 是圆周^2+(y)^2=2x位于 x 轴 上方的部分,则曲线积分^2+(y)^2=2x___
已知 L 是圆周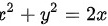 位于 x 轴 上方的部分,则曲线积分
位于 x 轴 上方的部分,则曲线积分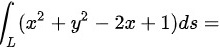 ___
___
题目解答
答案
∵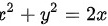
∴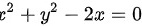 ,代入到曲线积分中
,代入到曲线积分中
∴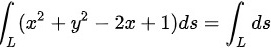
∵被积函数等式1时,第一类曲线积分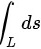 的几何意义是曲线段的弧
的几何意义是曲线段的弧
∴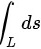 为相应的弧长
为相应的弧长
本题曲线为半圆,根据圆的求半径公式,当方程为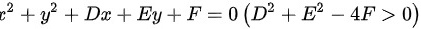 0\right)" data-width="426" data-height="29" data-size="5381" data-format="png" style="max-width:100%">
0\right)" data-width="426" data-height="29" data-size="5381" data-format="png" style="max-width:100%">
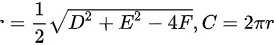 ,其中r为半径,C为周长
,其中r为半径,C为周长
对应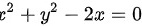 ,
,
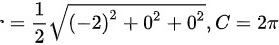
∵L 是圆周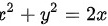 位于 x 轴 上方的部分,即半圆
位于 x 轴 上方的部分,即半圆
∴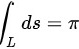
解析
步骤 1:化简圆周方程
给定的圆周方程为${x}^{2}+{y}^{2}=2x$,可以化简为${x}^{2}-2x+{y}^{2}=0$,进一步化简为${(x-1)}^{2}+{y}^{2}=1$。这表示圆心在(1,0),半径为1的圆。
步骤 2:代入曲线积分
将${x}^{2}+{y}^{2}-2x+1$代入到曲线积分中,得到${\int }_{L}^{(}{({x}^{2}+{y}^{2}-2x+1)ds$。由于${x}^{2}+{y}^{2}-2x=0$,所以${x}^{2}+{y}^{2}-2x+1=1$,因此曲线积分变为${\int }_{L}^{1}ds$。
步骤 3:计算曲线积分
由于${\int }_{L}^{1}ds$表示的是曲线L的弧长,而L是圆周${x}^{2}+{y}^{2}=2x$位于x轴上方的部分,即半圆。因此,${\int }_{L}^{1}ds$等于半圆的弧长,即$\pi$。
给定的圆周方程为${x}^{2}+{y}^{2}=2x$,可以化简为${x}^{2}-2x+{y}^{2}=0$,进一步化简为${(x-1)}^{2}+{y}^{2}=1$。这表示圆心在(1,0),半径为1的圆。
步骤 2:代入曲线积分
将${x}^{2}+{y}^{2}-2x+1$代入到曲线积分中,得到${\int }_{L}^{(}{({x}^{2}+{y}^{2}-2x+1)ds$。由于${x}^{2}+{y}^{2}-2x=0$,所以${x}^{2}+{y}^{2}-2x+1=1$,因此曲线积分变为${\int }_{L}^{1}ds$。
步骤 3:计算曲线积分
由于${\int }_{L}^{1}ds$表示的是曲线L的弧长,而L是圆周${x}^{2}+{y}^{2}=2x$位于x轴上方的部分,即半圆。因此,${\int }_{L}^{1}ds$等于半圆的弧长,即$\pi$。