题目
3.18设二维随机向量(X,Y)的分布函数为-|||-.F(x,y)= ) 1-(e)^-x-(e)^-y+(e)^-(x+y) 0, . , geqslant 0 ,geqslant 0 ,-|||-其他,-|||-讨论X,Y的独立性.
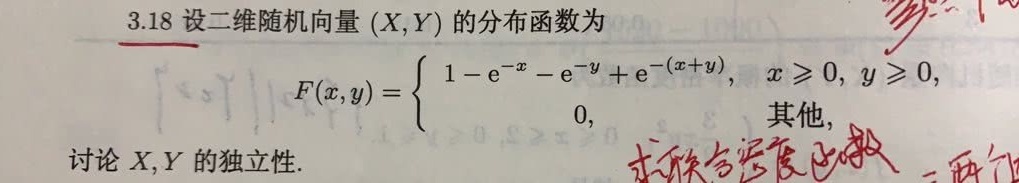
题目解答
答案

解析
考查要点:本题主要考查二维随机变量独立性的判断,需要掌握边缘分布函数的求法以及独立性的判定条件。
解题核心思路:
- 求边缘分布函数:通过联合分布函数分别求出$X$和$Y$的边缘分布函数$F_X(x)$和$F_Y(y)$。
- 验证乘积关系:检查是否对所有$x,y$有$F(x,y) = F_X(x) \cdot F_Y(y)$,若成立则$X$与$Y$独立。
破题关键点:
- 边缘分布函数的定义:$F_X(x) = F(x, +\infty)$,$F_Y(y) = F(+\infty, y)$。
- 指数函数的极限性质:当变量趋向$+\infty$时,$e^{-x} \to 0$。
求边缘分布函数$F_X(x)$
当$x \geq 0$时,取$y \to +\infty$:
$F_X(x) = F(x, +\infty) = 1 - e^{-x} - e^{-\infty} + e^{-(x+\infty)} = 1 - e^{-x}.$
当$x < 0$时,原式$F(x,y)=0$,故$F_X(x) = 0$。
求边缘分布函数$F_Y(y)$
同理,当$y \geq 0$时,取$x \to +\infty$:
$F_Y(y) = F(+\infty, y) = 1 - e^{-\infty} - e^{-y} + e^{-(\infty+y)} = 1 - e^{-y}.$
当$y < 0$时,$F_Y(y) = 0$。
验证独立性
对任意$x,y$,计算$F_X(x) \cdot F_Y(y)$:
- 当$x \geq 0$且$y \geq 0$时:
$F_X(x) \cdot F_Y(y) = (1 - e^{-x})(1 - e^{-y}) = 1 - e^{-x} - e^{-y} + e^{-(x+y)} = F(x,y).$ - 当$x < 0$或$y < 0$时,$F_X(x)$或$F_Y(y)$为$0$,乘积为$0$,与$F(x,y)$一致。
结论:对所有$x,y$,$F(x,y) = F_X(x) \cdot F_Y(y)$,故$X$与$Y$独立。