((1-sqrt {3)i)}^10的值为( )A.((1-sqrt {3)i)}^10B.((1-sqrt {3)i)}^10C.((1-sqrt {3)i)}^10D.((1-sqrt {3)i)}^10
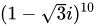 的值为( )
的值为( )
A.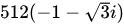
B.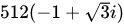
C.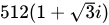
D.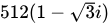
题目解答
答案
∵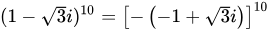
∴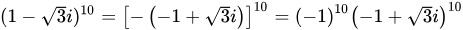
又∵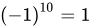
∴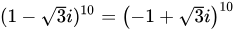
∵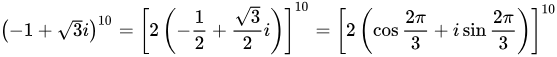
∴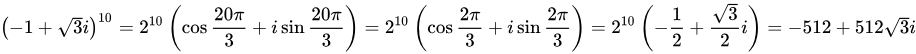
∴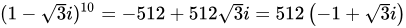
故答案选B。
解析
本题考查复数的高次幂运算,核心思路是将复数转换为极坐标形式,利用棣莫弗定理简化计算。关键在于:
- 确定复数的模和辐角;
- 应用棣莫弗定理计算幂;
- 化简角度至标准范围;
- 将结果转换为代数形式。
步骤1:转换复数形式
将复数 $1-\sqrt{3}i$ 转换为与 $-1+\sqrt{3}i$ 的关系:
$1-\sqrt{3}i = -(-1+\sqrt{3}i)$
步骤2:展开幂运算
利用幂的性质展开:
$(1-\sqrt{3}i)^{10} = [-(-1+\sqrt{3}i)]^{10} = (-1)^{10} \cdot (-1+\sqrt{3}i)^{10}$
由于 $(-1)^{10} = 1$,得:
$(1-\sqrt{3}i)^{10} = (-1+\sqrt{3}i)^{10}$
步骤3:转换为极坐标形式
计算 $-1+\sqrt{3}i$ 的模和辐角:
- 模:$\sqrt{(-1)^2 + (\sqrt{3})^2} = 2$
- 辐角:$\frac{2\pi}{3}$(第二象限)
因此:
$-1+\sqrt{3}i = 2\left(\cos\frac{2\pi}{3} + i\sin\frac{2\pi}{3}\right)$
步骤4:应用棣莫弗定理
计算 $10$ 次幂:
$(-1+\sqrt{3}i)^{10} = \left[2\left(\cos\frac{2\pi}{3} + i\sin\frac{2\pi}{3}\right)\right]^{10} = 2^{10} \left[\cos\left(10 \cdot \frac{2\pi}{3}\right) + i\sin\left(10 \cdot \frac{2\pi}{3}\right)\right]$
步骤5:化简角度
计算角度:
$10 \cdot \frac{2\pi}{3} = \frac{20\pi}{3} = 6\pi + \frac{2\pi}{3} \quad \Rightarrow \quad \text{等价于} \frac{2\pi}{3}$
步骤6:转换为代数形式
代入化简后的角度:
$2^{10} \left[\cos\frac{2\pi}{3} + i\sin\frac{2\pi}{3}\right] = 1024 \left(-\frac{1}{2} + i\cdot\frac{\sqrt{3}}{2}\right) = -512 + 512\sqrt{3}i = 512(-1+\sqrt{3}i)$