题目
求通过点M(3,1,-1)和M(3,1,-1)且平行于向量M(3,1,-1)的平面方程。
求通过点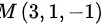
和
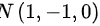且平行于向量
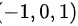的平面方程。
题目解答
答案
因为待求平面通过点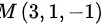和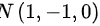，所以平面平行于向量
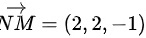，又因为平面平行于向量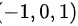，所以平面的法向量为
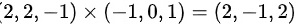，于是可以得到平面的点法式方程为
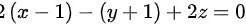，化简得到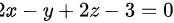
。
解析
步骤 1：确定向量$\overrightarrow {NM}$
向量$\overrightarrow {NM}$可以通过点M和N的坐标计算得到，即$\overrightarrow {NM} = (3-1, 1-(-1), -1-0) = (2, 2, -1)$。
步骤 2：计算平面的法向量
由于平面平行于向量$\overrightarrow {NM}=(2,2,-1)$和向量(-1,0,1)，平面的法向量可以通过这两个向量的叉乘得到。叉乘结果为$(2,2,-1)\times (-1,0,1) = (2,-1,2)$。
步骤 3：写出平面的点法式方程
已知平面的法向量为$(2,-1,2)$，且通过点N(1,-1,0)，可以写出平面的点法式方程为$2(x-1) - 1(y+1) + 2(z-0) = 0$，化简得到$2x - y + 2z - 3 = 0$。
向量$\overrightarrow {NM}$可以通过点M和N的坐标计算得到，即$\overrightarrow {NM} = (3-1, 1-(-1), -1-0) = (2, 2, -1)$。
步骤 2：计算平面的法向量
由于平面平行于向量$\overrightarrow {NM}=(2,2,-1)$和向量(-1,0,1)，平面的法向量可以通过这两个向量的叉乘得到。叉乘结果为$(2,2,-1)\times (-1,0,1) = (2,-1,2)$。
步骤 3：写出平面的点法式方程
已知平面的法向量为$(2,-1,2)$，且通过点N(1,-1,0)，可以写出平面的点法式方程为$2(x-1) - 1(y+1) + 2(z-0) = 0$，化简得到$2x - y + 2z - 3 = 0$。