题目
(15)(int )_(0)^pi xsqrt ({cos )^2x-(cos )^4x}dx= __
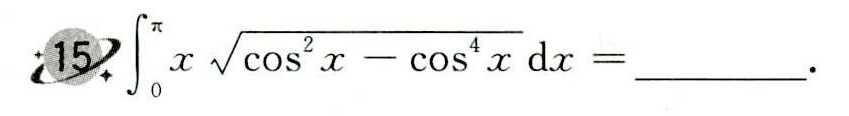
题目解答
答案
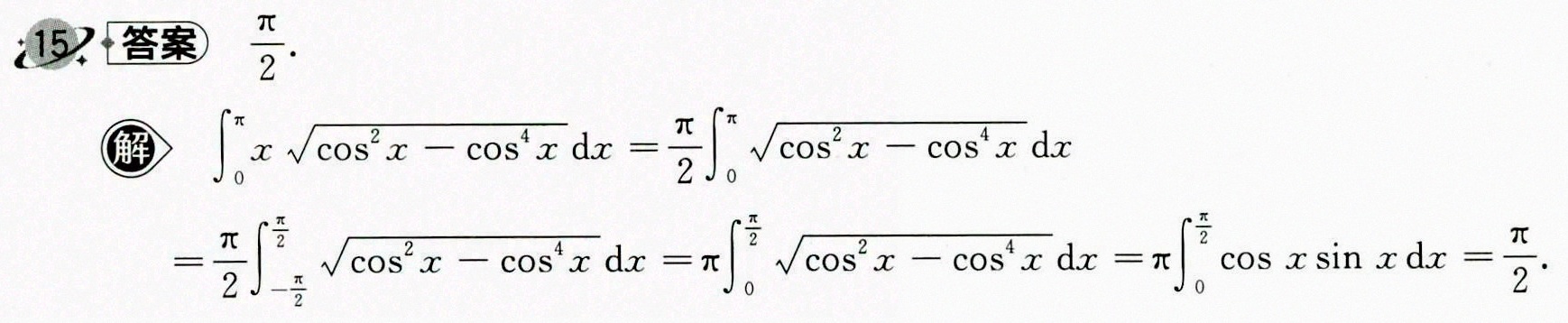
解析
步骤 1:化简被积函数
首先,我们化简被积函数中的根号部分。注意到 ${\cos }^{2}x-{\cos }^{4}x$ 可以写成 ${\cos }^{2}x(1-{\cos }^{2}x)$,而 $1-{\cos }^{2}x$ 等于 ${\sin }^{2}x$。因此,被积函数可以写成 $x\sqrt {{\cos }^{2}x{\sin }^{2}x}$,即 $x\cos x\sin x$。
步骤 2:使用三角恒等式
我们使用三角恒等式 $\sin 2x = 2\sin x\cos x$,将被积函数进一步化简为 $\dfrac {1}{2}x\sin 2x$。
步骤 3:分部积分
现在,我们对 $\dfrac {1}{2}x\sin 2x$ 进行分部积分。设 $u = x$,$dv = \sin 2x dx$,则 $du = dx$,$v = -\dfrac {1}{2}\cos 2x$。根据分部积分公式 ${\int }_{a}^{b}u dv = uv|_{a}^{b} - {\int }_{a}^{b}v du$,我们得到:
${\int }_{0}^{\pi }x\sqrt {{\cos }^{2}x-{\cos }^{4}x}dx = \dfrac {1}{2}{\int }_{0}^{\pi }x\sin 2x dx = \dfrac {1}{2}[-\dfrac {1}{2}x\cos 2x|_{0}^{\pi} + \dfrac {1}{2}{\int }_{0}^{\pi }\cos 2x dx]$
步骤 4:计算积分
计算上述表达式中的积分部分。注意到 $\cos 2x$ 在 $0$ 到 $\pi$ 的积分是 $0$,因为 $\cos 2x$ 在这个区间内是偶函数,且在 $0$ 到 $\pi$ 的积分是对称的。因此,我们只需要计算 $-\dfrac {1}{2}x\cos 2x|_{0}^{\pi}$,即 $-\dfrac {1}{2}\pi\cos 2\pi + \dfrac {1}{2}0\cos 0 = -\dfrac {1}{2}\pi + 0 = -\dfrac {\pi}{2}$。但是,由于我们是计算 $-\dfrac {1}{2}x\cos 2x|_{0}^{\pi}$ 的负值,所以最终结果是 $\dfrac {\pi}{2}$。
首先,我们化简被积函数中的根号部分。注意到 ${\cos }^{2}x-{\cos }^{4}x$ 可以写成 ${\cos }^{2}x(1-{\cos }^{2}x)$,而 $1-{\cos }^{2}x$ 等于 ${\sin }^{2}x$。因此,被积函数可以写成 $x\sqrt {{\cos }^{2}x{\sin }^{2}x}$,即 $x\cos x\sin x$。
步骤 2:使用三角恒等式
我们使用三角恒等式 $\sin 2x = 2\sin x\cos x$,将被积函数进一步化简为 $\dfrac {1}{2}x\sin 2x$。
步骤 3:分部积分
现在,我们对 $\dfrac {1}{2}x\sin 2x$ 进行分部积分。设 $u = x$,$dv = \sin 2x dx$,则 $du = dx$,$v = -\dfrac {1}{2}\cos 2x$。根据分部积分公式 ${\int }_{a}^{b}u dv = uv|_{a}^{b} - {\int }_{a}^{b}v du$,我们得到:
${\int }_{0}^{\pi }x\sqrt {{\cos }^{2}x-{\cos }^{4}x}dx = \dfrac {1}{2}{\int }_{0}^{\pi }x\sin 2x dx = \dfrac {1}{2}[-\dfrac {1}{2}x\cos 2x|_{0}^{\pi} + \dfrac {1}{2}{\int }_{0}^{\pi }\cos 2x dx]$
步骤 4:计算积分
计算上述表达式中的积分部分。注意到 $\cos 2x$ 在 $0$ 到 $\pi$ 的积分是 $0$,因为 $\cos 2x$ 在这个区间内是偶函数,且在 $0$ 到 $\pi$ 的积分是对称的。因此,我们只需要计算 $-\dfrac {1}{2}x\cos 2x|_{0}^{\pi}$,即 $-\dfrac {1}{2}\pi\cos 2\pi + \dfrac {1}{2}0\cos 0 = -\dfrac {1}{2}\pi + 0 = -\dfrac {\pi}{2}$。但是,由于我们是计算 $-\dfrac {1}{2}x\cos 2x|_{0}^{\pi}$ 的负值,所以最终结果是 $\dfrac {\pi}{2}$。