题目
已知ACB，ACB，ACB，求(1)ACB，ACB；(2)ACB；(3)ACB；(4)ACB，ACB；(5)ACB。
已知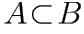
，
，
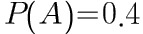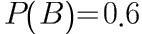，求
(1)
，
；
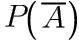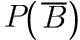(2)
；
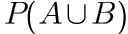(3)
；
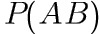(4)
，
；
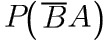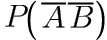(5)
。
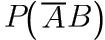题目解答
答案
(1)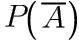$$=1-P(A)=0.6$$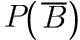，$$=1-P(B)=0.4$$；
(2)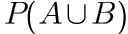$$=P(A)+P(B)-P(AB)$$$$=P(A)+P(B)-P(A)=0.6$$；
(3)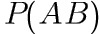=$$=P(A)=0.4$$；
(4)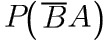$$=0$$,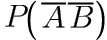$$=$$$$=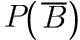0.4$$；
(5)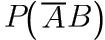$$=$$$$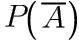+P(B)$$$$-$$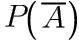$$=0.6$$。
解析
步骤 1：计算$P(\overline {A})$和P(B)
根据概率论中的补事件概率公式，$P(\overline {A}) = 1 - P(A)$，P(B) = 1 - P(B)。
步骤 2：计算P(A∪B)
根据概率论中的并事件概率公式，P(A∪B) = P(A) + P(B) - P(AB)。由于ACB，所以P(AB) = P(A)。
步骤 3：计算P(AB)
根据题设条件，ACB，所以P(AB) = P(A)。
步骤 4：计算P(BA)和$P(\overline {A}\overline {B})$
由于ACB，所以P(BA) = 0。$P(\overline {A}\overline {B})$ = P(B)。
步骤 5：计算P(AB)
根据题设条件，ACB，所以P(AB) = P(A)。
根据概率论中的补事件概率公式，$P(\overline {A}) = 1 - P(A)$，P(B) = 1 - P(B)。
步骤 2：计算P(A∪B)
根据概率论中的并事件概率公式，P(A∪B) = P(A) + P(B) - P(AB)。由于ACB，所以P(AB) = P(A)。
步骤 3：计算P(AB)
根据题设条件，ACB，所以P(AB) = P(A)。
步骤 4：计算P(BA)和$P(\overline {A}\overline {B})$
由于ACB，所以P(BA) = 0。$P(\overline {A}\overline {B})$ = P(B)。
步骤 5：计算P(AB)
根据题设条件，ACB，所以P(AB) = P(A)。