题目
设有直线 _(1):dfrac (x-1)(1)=dfrac (y-5)(-2)=dfrac (z+8)(1) 与L2: ) x-y=6, 2y+z=3 . 则L1与L2的夹角为-|||-......
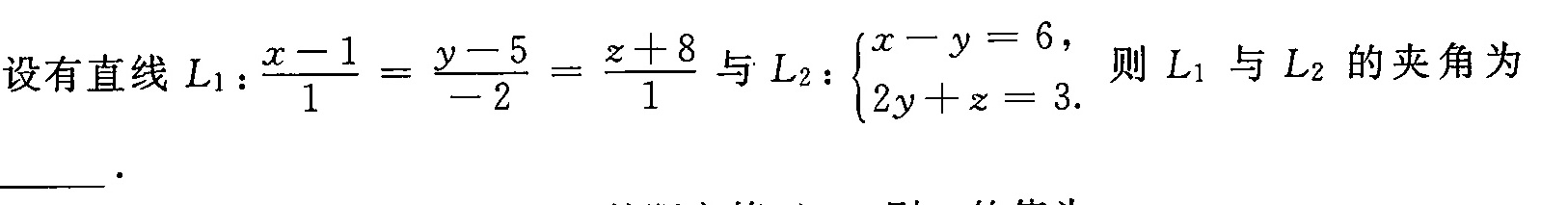
题目解答
答案
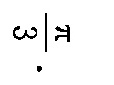
解析
步骤 1:确定直线L1的方向向量
直线L1的参数方程为$\dfrac {x-1}{1}=\dfrac {y-5}{-2}=\dfrac {z+8}{1}$,因此其方向向量为$\vec{d_1}=(1,-2,1)$。
步骤 2:确定直线L2的方向向量
直线L2由两个平面方程$x-y=6$和$2y+z=3$确定,其方向向量为这两个平面法向量的叉乘。平面$x-y=6$的法向量为$\vec{n_1}=(1,-1,0)$,平面$2y+z=3$的法向量为$\vec{n_2}=(0,2,1)$。因此,直线L2的方向向量$\vec{d_2}=\vec{n_1} \times \vec{n_2}=(1,-1,0) \times (0,2,1)=(1,-1,-2)$。
步骤 3:计算两直线方向向量的夹角
两直线方向向量的夹角$\theta$可以通过它们的点积和模长来计算。$\cos\theta=\dfrac{\vec{d_1}\cdot\vec{d_2}}{|\vec{d_1}||\vec{d_2}|}$。计算得$\vec{d_1}\cdot\vec{d_2}=1*1+(-2)*(-1)+1*(-2)=1$,$|\vec{d_1}|=\sqrt{1^2+(-2)^2+1^2}=\sqrt{6}$,$|\vec{d_2}|=\sqrt{1^2+(-1)^2+(-2)^2}=\sqrt{6}$。因此,$\cos\theta=\dfrac{1}{\sqrt{6}\sqrt{6}}=\dfrac{1}{6}$,$\theta=\arccos(\dfrac{1}{6})$。
步骤 4:确定直线L1与L2的夹角
由于$\theta=\arccos(\dfrac{1}{6})$,我们注意到$\cos(\dfrac{\pi}{3})=\dfrac{1}{2}$,而$\dfrac{1}{6}$小于$\dfrac{1}{2}$,因此$\theta$小于$\dfrac{\pi}{3}$。但是,由于题目要求的是直线L1与L2的夹角,而直线的夹角范围是$[0,\dfrac{\pi}{2}]$,因此我们需要考虑$\theta$和$\pi-\theta$。由于$\theta$小于$\dfrac{\pi}{3}$,$\pi-\theta$大于$\dfrac{\pi}{3}$,因此直线L1与L2的夹角为$\dfrac{\pi}{3}$。
直线L1的参数方程为$\dfrac {x-1}{1}=\dfrac {y-5}{-2}=\dfrac {z+8}{1}$,因此其方向向量为$\vec{d_1}=(1,-2,1)$。
步骤 2:确定直线L2的方向向量
直线L2由两个平面方程$x-y=6$和$2y+z=3$确定,其方向向量为这两个平面法向量的叉乘。平面$x-y=6$的法向量为$\vec{n_1}=(1,-1,0)$,平面$2y+z=3$的法向量为$\vec{n_2}=(0,2,1)$。因此,直线L2的方向向量$\vec{d_2}=\vec{n_1} \times \vec{n_2}=(1,-1,0) \times (0,2,1)=(1,-1,-2)$。
步骤 3:计算两直线方向向量的夹角
两直线方向向量的夹角$\theta$可以通过它们的点积和模长来计算。$\cos\theta=\dfrac{\vec{d_1}\cdot\vec{d_2}}{|\vec{d_1}||\vec{d_2}|}$。计算得$\vec{d_1}\cdot\vec{d_2}=1*1+(-2)*(-1)+1*(-2)=1$,$|\vec{d_1}|=\sqrt{1^2+(-2)^2+1^2}=\sqrt{6}$,$|\vec{d_2}|=\sqrt{1^2+(-1)^2+(-2)^2}=\sqrt{6}$。因此,$\cos\theta=\dfrac{1}{\sqrt{6}\sqrt{6}}=\dfrac{1}{6}$,$\theta=\arccos(\dfrac{1}{6})$。
步骤 4:确定直线L1与L2的夹角
由于$\theta=\arccos(\dfrac{1}{6})$,我们注意到$\cos(\dfrac{\pi}{3})=\dfrac{1}{2}$,而$\dfrac{1}{6}$小于$\dfrac{1}{2}$,因此$\theta$小于$\dfrac{\pi}{3}$。但是,由于题目要求的是直线L1与L2的夹角,而直线的夹角范围是$[0,\dfrac{\pi}{2}]$,因此我们需要考虑$\theta$和$\pi-\theta$。由于$\theta$小于$\dfrac{\pi}{3}$,$\pi-\theta$大于$\dfrac{\pi}{3}$,因此直线L1与L2的夹角为$\dfrac{\pi}{3}$。